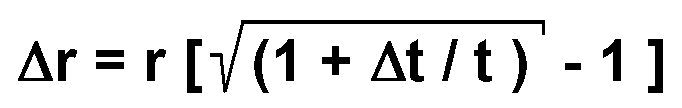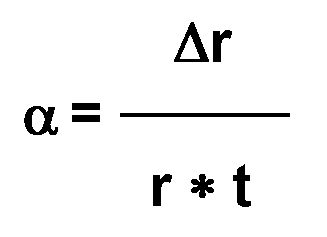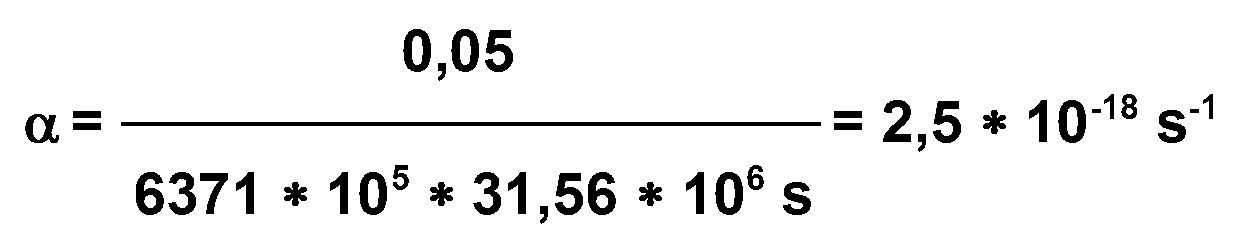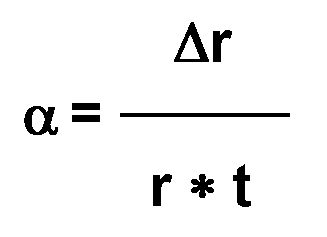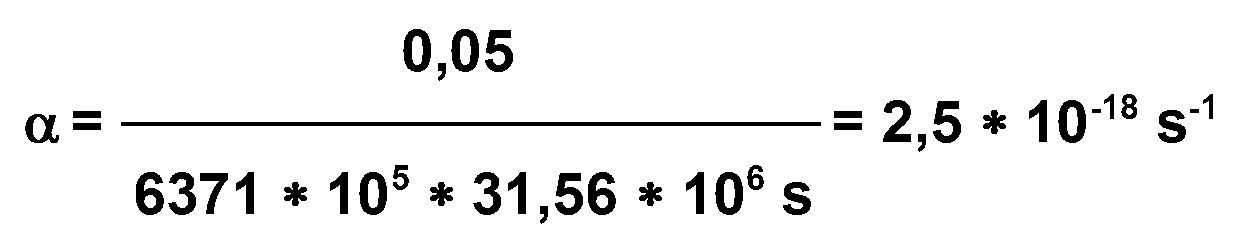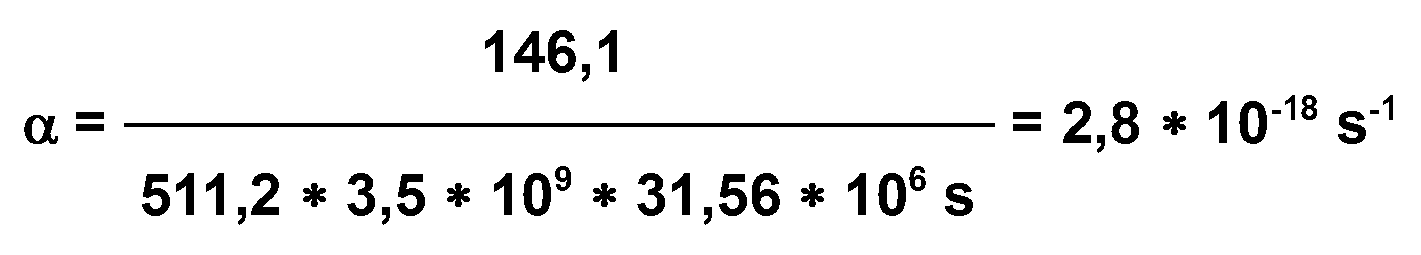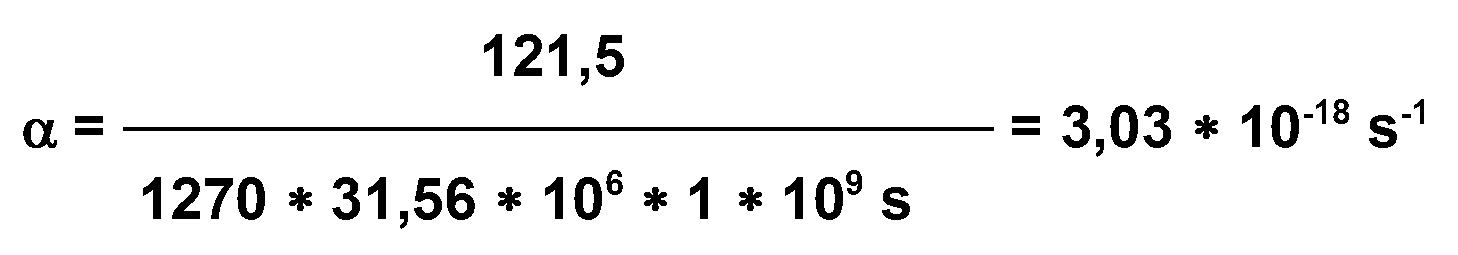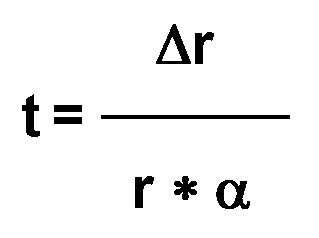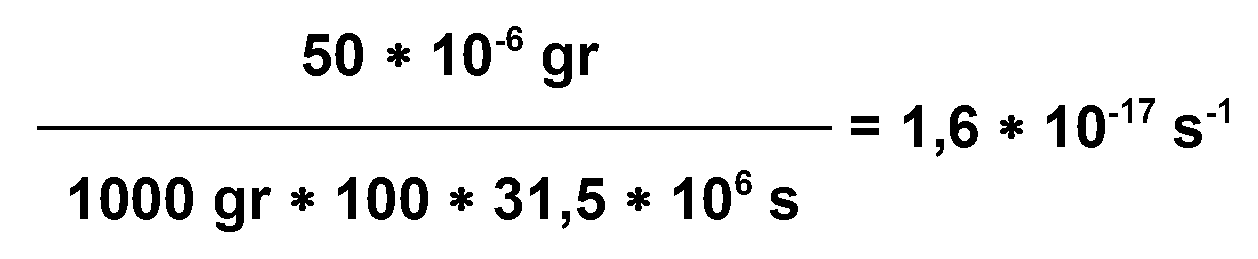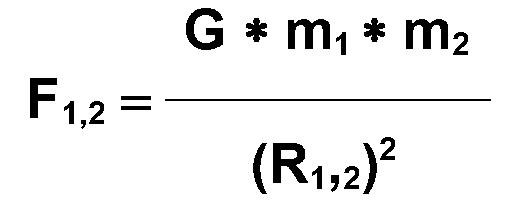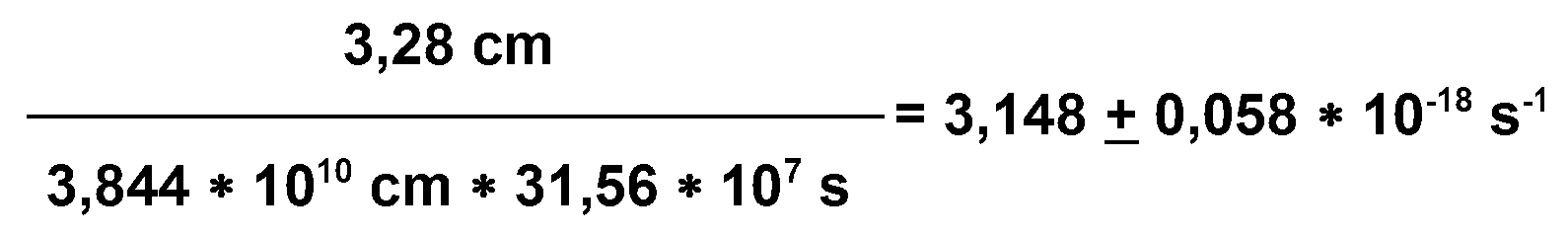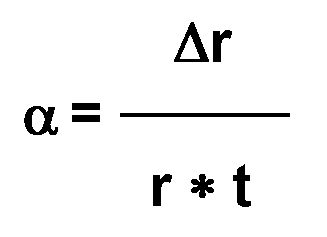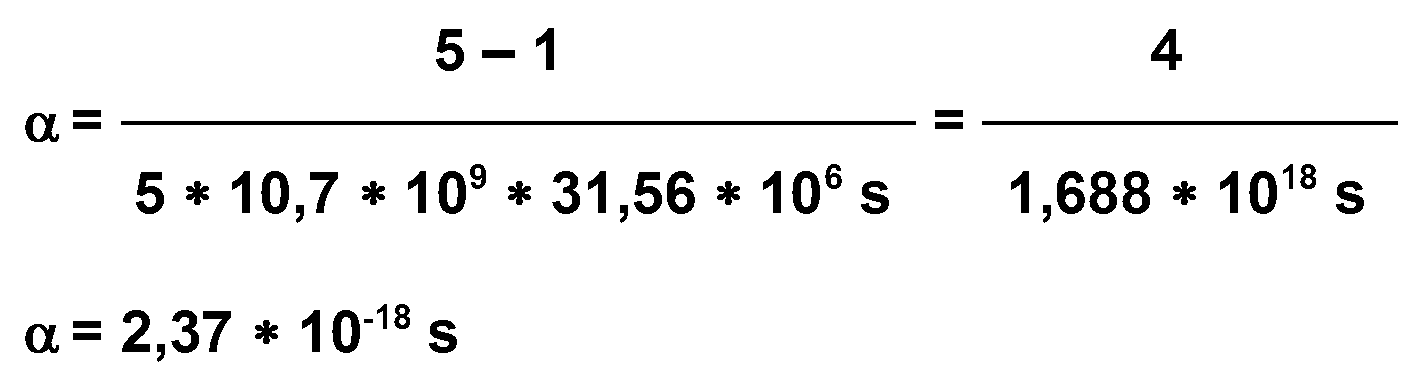Juni
2010
Volkmar
Müller
Inhalt
Abstract
1.
Einleitung
2. Die
Rotationsverzögerung der Erde
3. Das
Trägheitsmoment des Erde-Mond-Systems
4. Die
Expansion der Erde
5.
Postglaziale Landhebung der Erde
6.
Meeresspiegelanstieg durch Klimaänderung
7. Der
innere Erdkern
8.
Erdoberfläche und Alter der Kontinente
9.
Subduktion
10.
Urkilogramm
11.
Gezeitenreibung - Ursache der Rotationsverzögerung?
12. Die
Expansion des Mondorbits
13. Mars
14. Die
Pioneeranomalie
15.
Pulsare
16.
Hyperaktive Galaxien des frühen Universums
17.
Diskussion
18.
Zusammenfassung / Summary
Zusammenstellung
relevanter Werte
Literatur
Abstract
Mit
einer Reihe von Beispielen wird belegt, daß die kosmologische
Expansion auch in Bereichen stattfindet, in denen es keine
kosmologische Expansion geben sollte. Vorausgesetzt ist die
Verwendung der SI-Metrik. Benutzt man die UT-Skala, so
entfällt
die kosmologische Expansion sowie der Big Bang. Probleme, welche
durch das Benutzen der SI-Skala entstehen, entfallen bei Anwendung
der UT-Skala. Dazu gehört zum Beispiel die Dichte einer
expandierenden, jungen Erde. Auch die Dynamik und Dichte von
hyperaktiven, Galaxien im frühen Universum gehören
dazu.
Einige Phänomene legen es nahe die UT-Skala statt der SI-Skala
anzuwenden.
With
a
number of examples show that the cosmological expansion occurs evenin
areas where there should be no cosmological expansion. Theapplication
of the SI-metrics is prerequisite. If you use the UT-scale one, the
cosmological expansion is inapplicable so. Thiseliminates the Big
Bang. Problems that arise from the use of the SIscale omitted when
applying the UT scale. This includes, for example, the density of an
expanding, young Earth. Also the dynamism anddensity of hyperactive,
galaxies in the early universe belong to it. The application of that
UT - scale is partially more advantageous than the SI - scale.
Schlüsselworte
Zeitsysteme,
Erdexpansion, weitere Expansionseffekte, entfernungsproportionale
kosmologische Expansion.
1.
Einleitung
Man
postulierte eine Grenze, unterhalb welcher die universelle Expansion
nicht stattfindet. Diese Grenze soll oberhalb gravitativ gebundener
Systeme liegen. Der Autor dieser Arbeit geht im Gegensatz dazu davon
aus, daß diese Grenze unterhalb gravitativ dominierter
Systeme
liegt. Diese gegensätzliche Ansicht resultiert aus dem
mehrfachen Auftauchen des Hubble-Parameters bzw. der kosmologischen
Expansionsrate in Bereichen, in denen das entsprechend der
Standardtheorie nicht sein kann. Die Erde als Ganzes ist
gravitativdominiert (andere Naturkräfte spielen für
die
Erde eine untergeordnete Rolle). Nach Ansicht des Autors
verhält
sich die Erde hinsichtlich der kosmologischen Expansion wie das
Universum. Kleinere Gegenstände werden meist durch andere
Kräfte
dominiert und expandieren dann nicht. Bei Asteroiden ist die
Eigengravitation zu gering um sie in die Kugelform zu
zwingen,Kristalline / Molekulare Kräfte also
elektromagnetische
Kräfte dominieren.
In
der Arbeit wird festgestellt, daß die säkulare
Verzögerungsrate der Erdrotation von annähernd
gleicher
Größe wie die Expansionsrate von Universum und
Mondbahn
ist. Die Ursachen der Gezeitenreibung werden erklärt, wobei
die
Berechnungen die Größe der gemessenen
Rotationsverzögerung
der Erde ausschließen. Nur die Expansion der Erde wird als
Möglichkeit gesehen deren Rotationsverzögerung zu
begründen.
In einer Reihe
von Abschnitten werden Indizien aufgeführt, die für
eine
Expansion der Erde mit einer Expansionsrate sprechen, die gleich der
kosmologischen Expansionsrate ist. Diese Expansionsrate ist
für
die Geo-Wissenschaften besser akzeptabel als die von Vertretern der
„Schnellen Erdexpansion“ geforderte Expansionsrate.
Die
kosmologische Expansion wird für die in der
Arbeit
beschriebenen Expansions- und Retardationseffekte verantwortlich
gemacht. Es werden Beispiele für solche Effekte
abgeschätzt,die
nicht vom System der Erde verursacht sind. Die Expansion der Erde
wird als wesensgleich der kosmologischen Expansion angenommen. Dies
ist jedoch im Rahmen der Friedmanschen Kosmologie (Big Bang) nicht
möglich. Es wird dargestellt, daß die Weltzeitskala
(UT)
eine kosmologische Bedeutung besitzt und auf ein raum-zeitlich
unbegrenztes Universum führt in welchem das kosmologische
Expansionsverbot für die Erde nicht besteht. Hinsichtlich der
kosmologischen Expansion wird eine andere untere Schranke
postuliert,deren Auftreten in den weiteren Kapiteln erläutert
ist. In diesen Kapiteln werden auch die Konsequenzen des Auftretens
von zwei Zeitskalen für die Kosmologie und die Erdexpansion in
kurzen Zügen abgehandelt. Dazu gehört z.B.,
daß die
Expansion einen imaginären Charakter hat und sich der Raum
ausdehnt ohne daß sich die Entfernungen ändern. Die
Erde
expandiert ohne ihre numerische Dichte, Rotationszeit oder
Durchmesser zu ändern.
2.
Die Rotationsverzögerung der Erde und die variable Weltzeit
In
einem Jahr durchläuft die Sonne scheinbar die ganze
Ekliptik. Das
heißt, ihre Länge nimmt in 24 Sekunden um eine
Bogensekunde zu. Der Mond ist ca. 12 mal schneller und deshalb
für
Zeitbestimmungen besser geeignet. Bereits Halley konnte dadurch 1693
die Akzeleration des Mondes an Hand alter Aufzeichnungen bemerken.
Schwerpunkte
für die Abweichungen in Länge liegen in der Abnahme
der
Erdbahnexentrizität, in der Präzession und in der
Rotationsverzögerung der Erde. Neben diesen Variationsursachen
gibt es noch weitere die allerdings langfristig kleinere Auswirkungen
besitzen. Die Rotationsverzögerung allein bewirkt,
daß die
Länge der Sonne in 100 Jahren um mehr
als 1 Bogensekunde gegenüber der berechneten Länge zu
groß
ist. Das entspricht 29.2208 Zeitsekunden, welche die mittlere
Sonnenzeit gegenüber der berechneten nachgeht.
Die
Rotationsverzögerung der Erde war überhaupt der
ausschlaggebende Grund für die Einführung einer
anderen
Zeitskale, der Ephemeridenzeit (ET). Die, von Schwankungen
abgesehen, nachgehende "Erduhr" läuft seit Beginn der
Berechnungsgrundlage der ET, das heißt seit dem Jahr
1900, bereits um mehr als eine Minute nach. Damit die GMT bzw.
Weltzeit (UT) und die ET nicht immer mehr auseinander laufen, wurde
1972 die "Koordinierte Weltzeit" (UTC) eingeführt. Zum
Angleichen beider Zeitskalen werden hier halbjährlich bei
Bedarf
Schaltsekunden eingefügt bzw. weggelassen. Man verzichtet also
auf die Definition der Weltzeitsekunde (nicht der Sekunde!) als
1/86400 Tag, wie noch deutlicher gezeigt werden soll.
Als
die Verzögerung der Erdrotation noch nicht bekannt war,
konnten
die beiden Zeitskalen natürlich auch noch nicht angeglichen
werden. Bei der Nachberechnung alter Finsternisaufzeichnungen stellte
sich unter Beachtung der Randbedingungen (z.B. Kalenderreformen)
heraus, daß Zeit und Ort der Aufzeichnungen der Finsternisse
nicht mit den Ergebnissen der Rechnungen übereinstimmen. Die
ungenauen Zeitmessungen von damals gestatten zwar eine gewisse
Toleranz hinsichtlich des genauen Zeitpunktes, nicht aber
hinsichtlich des Beobachtungsortes, der bei totalen
Sonnenfinsternissen einen schmalen Streifen auf der
Erdoberfläche
bildet. Ein Ereignis, welches z.B. in Griechenland beobachtet wurde,
muß logischerweise auch dort stattgefunden haben und nicht
entsprechend nachträglicher Berechnung in Spanien (siehe Abb.
1).
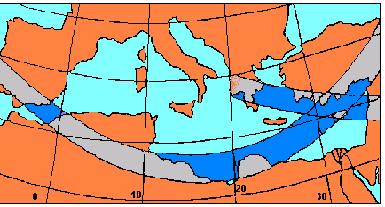
Abb. 1:
Verlauf der totalen Sonnenfinsternis vom 14. Jan. 484 n.C. und ihre
nachberechnete Lage bei unverzögerter Erdrotation (links)
Weicht
der Beobachtungsort von der Nachberechnung um z.B. 30
Längengrade
ab, so ist aus der Rotationsgeschwindigkeit von 15 Grad pro Stunde auf
eine Rotationsverzögerung von 2 Stunden seit dem Eintritt der
Finsternis zu schließen. Das heißt, seit der
Finsternis
sind 2 * 3600 Weltzeitsekunden mehr vergangen als
Ephemeridenzeitsekunden bzw. SI-Sekunden.
Die
Skalen der Weltzeitsekunden und der SI-Sekunden laufen nicht
synchron. Die Definition von 2 verschiedenen Sekunden ist somit
wichtig und nicht verzichtbar.
Die
aufsummierte Zeitdifferenz beider Zeitskalen Δt
läßt
sich
z.B. mit Hilfe einer Gleichung, die Ahnert (1959) angibt, berechnen:
Δt
= 24,349 + 72,318 T + 29,95 T2 + 1,821 B
Gleichung
2.1: T
wird in julianischen Jahrhunderten eingesetzt, das absolute und erste
lineare Glied sind Angleichungswerte, das quadratische Glied
beschreibt die stetige, säkulare Rotationsverzögerung
der
Erde und das letzte lineare Glied kann nur nachträglich durch
Beobachtungen bestimmt werden.
Es ist unregelmäßig
schwankend und nicht additiv.
Infolge
der Unregelmäßigkeit des letzten Gliedes ist eine
Vorausberechnung von Δt nicht möglich. Diese
Unregelmäßigkeiten
sind teils sporadischer und teils periodischer Natur. Ihre Ursachen
liegen in der Erdbebentätigkeit, jahreszeitlichen
Temperatureinflüssen, Vegetationsperioden u.a.m. Alle diese
Einflüsse werden bei den weiteren Betrachtungen
außer Acht
gelassen. Einzig die Ursachen, die zur
säkularen
Rotationsverzögerung beitragen können werden
näher
untersucht.
Beachtet
man die Verlängerung des Tages die von Bär (2008) mit
0,0016 Sekunden in 100 Jahren angegeben ist, so kann man schreiben:
Δt
= 29,2208 * T2
Gleichung
2.2: Δt
= in Sekunden, T = Anzahl Julianischer Jahrhunderte
Die
Rotationsverzögerung hält offensichtlich auch
über
geologisch bedeutsame Zeiträume hinweg an. Es fanden sich
fossile Organismen aus den geologischen Epochen von der Kreide bis
zum Kambrium, die Jahreswachstumsringe und diesen aufgeprägte
Tageswachstumsringe zeigen .
Aus diesen Organismen lassen sich auch
Rückschlüsse
über die damalige Länge des Monats und den
Gezeitentyp am
Wachstumsort ziehen. Durch Auszählung konnte ermittelt werden,
daß ältere Formen mehr Tagesringe pro Jahresring
zeigen
als jüngere. 380 Millionen Jahre alte Korallen aus dem Devon
zeigen z.B. pro Jahresring 396 Tagesringe. Die Erde rotierte damals
396 mal im Jahr.
Wird
nun, nicht auf der Basis von Schaltsekunden, sondern mit variablen
UT-Sekunden, die Zeitdifferenz zwischen UT und ET für diese
380 Millionen Jahre errechnet, so sieht dies unter der Voraussetzung
einer konstanten Jahreslänge wie folgt aus:
Das
Jahr hat 31,6 * 106
Sekunden.
Für den Tag bleiben damals ca. 79700 (ET)-Sekunden. Die
damalige
UT-Sekunde war demnach gleich 79700 / 86400 = 0,92 der Länge
der
heutigen Sekunde. Die in den 380 * 106
Jahren
aufsummierte Differenz zwischen UT und ET (TAI) ergibt sich aus:
Σ =
0,5 n ( x1 +
xn )
=
0,5 * 120,1 * 1014
*
( 1 + 0,922 ) = 115,4 * 1014
Gleichung 2.3: Σ =
Zeitraum in SI-Sekunden, n = Zeitraum in UT-Sekunden, x1
=
Länge rezente Sekunde (1,0), xn
=
Länge der ersten Sekunde (0,92)
Δt =
( ET - UT )
=
115,4 * 1014 - 120,1 * 1014 =
- 4,7 * 1014
Gleichung 2.4
Dabei
wurde die SI-Sekunde mit der ET-Sekunde identifiziert. Wendet
man, unabhängig von den aufgefundenen Korallen,
Gleichung 2.1
unter Vernachlässigung des letzten Gliedes
für den
gleichen Zeitraum an, so erhält man Δt = 4,3 * 1014
Sekunden. Das
gute Zusammenpassen der beiden unabhängig voneinander
gefundenen
Werte für Δt sichert die Anwendbarkeit von Gleichung 2.2
und die relative Konstanz der
Rotationsverzögerung für
den gegebenen Zeitraum. Im Zeitraum von 380 Millionen Jahren sind ca.
4,7 * 1014 UT-Sekunden mehr vergangen als
SI-Sekunden. Das
sind 14,9 Millionen Jahre!
Bei
Benutzung von Schaltsekunden bedeutet das, daß im
Durchschnitt
jede 25. Sekunde eine Schaltsekunde hätte sein
müssen. Immer
vorausgesetzt, daß die Schaltsekunden nur aus der
Rotationsverzögerung resultieren, was streng genommen nicht
der
Fall ist. Die Definitionsabweichung der UT-Sekunde als 1/86400 Tag
wird hier deutlich. Unter Beachtung der Länge des Julianischen
Jahrhunderts von ca. 31,56 * 108
Sekunden
kann
mittels des quadratischen Gliedes aus Gleichung 2.2 die rezente
Verzögerungsrate
α
der
Erdrotation
bestimmt werden:
α = 29,22 * T2
α = 29,2208 ( 1 /
31,56
* 108 )2
α =
2,93 * 10-18 s-1
Gleichung 2.5
Dieser
Wert resultiert aus dem Beobachtungswert für die
Tagesverlängerung von 0,0016 s / 100 a.
Die
Verzögerungsrate
der Erdrotation ist annähernd von der Größe
der
Expansionsrate des Universums.
Die
Größe dieses Parameters
beträgt
nach Messungen von WMAP = 2,30 ±
0,26 * 10-18
s-1. Akzeptabel sind jedoch auch Werte, die
diese
Toleranz
etwas überschreiten.
3.
Das Trägheitsmoment des Erde-Mond-Systems
Abgesehen
von Einflüssen der Sonne und der Planeten sollte das
gemeinsame
Trägheitsmoment (Drall) von Erde + Mond konstant sein. Die
verzögerte Erdrotation läßt also folgende
Ursachen
zu:
1.
Der Mond übernimmt einen Teil des Dralls der Erde.
2. Die Erde dehnt sich aus.
3. Es besteht eine Kombination vorgenannter Varianten.
Eine
Reihe von Leuten geht davon aus, daß die 1. Variante
realisiert
ist. Der Impulstransfer soll durch Gezeitenreibung zustande kommen
(siehe Abschnitt 11).
Wenn
die Rotationsverzögerung der Erde zum wesentlichen Teil durch
Expansion verursacht sein sollte, so läßt sich die
Größe
der Expansion mit dem Drallsatz berechnen:
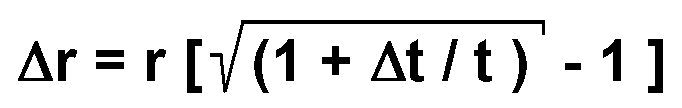
Gleichung 3: Δr
= Radiusdifferenz,
r = Erdradius, t
= Zeitraum, Δt
= Zeitdifferenz ET-UT
Δr
= 6371 * 105 [ ( 1+
0,0016
/ 86400 )0,5 -1 ]
= 5,9 cm
Gleichung 3.1
Für
den Erdradius sei 6371 * 105
cm gesetzt. Der
berechneten Differenz des Erdradius wurde hier die Änderung
der
Tageslänge in 100 Jahren zugrunde gelegt, es ergibt sich somit
auch die Radiusänderung für 100 Jahre. Im
Klammerausdruck ist die Änderung der Länge eines
Tages pro
Jahrhundert angegeben.
Die
Rotationsverzögerung der Erde entspricht einer Expansion des
Erdradius 0,059 cm / a.
Viele
Anhänger der Erdexpansion gehen davon aus, daß die
Erdexpansion zur Zeit » 2cm / Erdradius und Jahr
beträgt.
Das entspricht einer Expansionsrate von ca. 1 * 10-16
s-1.
Da die Verzögerungsrate der Erde nicht 1 * 10-16 s-1,
sondern 3,0 * 10-18 s-1 beträgt,
muß
angenommen werden, daß der von Maxlow, Koziar u.a. bevorzugte
Wert für die Erdexpansion falsch ist. Mehrere Autoren (und
Meßergebnisse) stimmen deswegen auch nicht mit diesem
Expansionswert überein und man distanziert sich generell von
einer Erdexpansion.
Die
Erdexpansion von ca. 2 cm pro Radius und Jahr erfährt auch aus
diesem Grund keine Anerkennung!
4.
Die Expansion der Erde
Nachdem
die Idee der Drift der Kontinente Afrika und Südamerika durch
A.
Wegener verbreitet war befaßten sich viele Leute mit dieser
Idee.
Es blieb nicht aus, daß sie auch auf andere Kontinente
probeweise
angewendet wurde und es stellte sich heraus, daß auch andere
Kontinente infolge ihrer Küstenlinien oder anderer Merkmale
zusammen passten. Hilgenberg ging bereits 1933 von einer expandierenden
Erde aus. 1935 vermutete Halm eine Verwandtschaft von Erdexpansion und
Expansion des Universums. Durch Keindl wurde 1940 ebenfalls eine
expandierende Erde mit abnehmender Dichte angenommen.Die Ideen
scheiterten offensichtlich an den unrealistischen Konsequenzen.
Unwiderlegt blieben die Ansichten von P. Dirac und P. Jordan
hinsichtlich einer Abnahme der Gravitationskonstante was ebenfalls zu
Expansionseffekten bei Erde und Universum führt.Diese
Möglichkeit wird in dieser Arbeit nicht
erforderlich.Schließlich gelang diese Zusammenpassung
über
alle Ozeane für alle Kontinente. Durch O. C. Hilgenberg wurde
erstmals ein Globus erstellt, der keine Ozeane zwischen den Kontinenten
hatte. Inzwischen hat man erreicht, daß 95 % der
kontinentalen
Flächen unter Einbeziehung der Schelfgebiete zueinander
passen.
Die Folge dieses Befundes ist, daß der Globus nur aus
Kontinentalplatten mit einem Radius von ca. 55 - 60 % des
tatsächlichen Radius besteht. Der scheinbare Befund,
daß die
ozeanischen Böden kaum über 200 Millionen Jahre alt
sind
ergab dann ein Bild, welches nach Carey, Maxlow und Anderen einen
exponentiell expandierenden Erdradius zeigte. Der zeitliche Beginn
dieser Expansion lag vermutlich im Perm. Eine Ursache ist nicht bekannt.
Seit den neunziger Jahren des vergangenen Jahrhunderts bekam man die
Möglichkeit der Messung der Driftraten der Kontinente. Diese
Driftraten widersprechen dem skizzierten Bild der Erdexpansion absolut
nicht, wenn auf Subduktionszonen verzichtet wird. Spätestens
hier
gab es jedoch keine Übereinstimmung mit der Plattentektonik
mehr.
Es
gab aber auch andere Ansichten, die eine Erdexpansion
befürworteten. Hier sind Egyed (1969), Schmutzer (2000) und
Owen
zu nennen. Die Expansionrate ist nach deren Arbeiten wesentlich kleiner
und auch über längere Zeiträume hinweg zu
verfolgen. Die
Auseinandersetzung mit Plattentektonikern ist darum weniger hart.
Es
gibt also nach dem Willen ihrer Verfechter eine schnelle, exponentielle
Erdexpansion und eine langsame. Während die Vertreter der
schnellen Expansion eine Rate von ca. 2 cm pro Jahr und Erdradius annehmen,
favorisieren andere eine Expansionsrate von ca. 0,05 cm / a und
Erdradius. Beide Richtungen nutzen zum Teil die gleichen Argumente
für eine Erdexpansion. Leider ignorieren sie zum Teil auch
Argumente was wiederum von der Plattentektonik genutzt wird um gegen
eine Erdexpansion zu argumentieren. Gute und weniger gute Argumente und
Hinweise haben alle:
Gegen
eine Expansion sprechen eine wahrscheinlich konstante Erdmasse und das
offensichtliche Vorhandensein von Subduktionszonen. Es gibt weitere
Befunde, welche sich zum Teil auch nur gegen eine Art der Expansion
richten. Für eine Expansion spricht zum Beispiel die gute
Paßgenauigkeit der Kontinente. Dieser Effekt ist durch andere
Annahmen als Expansion nicht erklärbar.
Weitere
Expansionshinweise sind:
- Obwohl
sich der Atlantik und der Indik ausbreiten, findet man in Ostafrika
ausgedehnte Zerrungsgebiete in Form der ostafrikanischen
Grabenbrüche. Eigentlich sind Faltungsgebiete zu erwarten.
- Verschiedene
Gesteine, die magnetische Mineralien enthalten nehmen bei der
Abkühlung unter die Curietemperatur die Magnetisierung des
Erdmagnetfeldes an und können diese sehr lange behalten,
solange
sie nicht erneut erwärmt werden. Unter Beachtung gewisser
Einflußfaktoren kann man aus der Inklination der magnetischen
Gesteine eines Kontinentalblockes Rückschlüsse auf
die Lage
der magnetischen Pole zur Zeit der Gesteinsentstehung ziehen.
Gleichzeitig werden Rückschlüsse auf die Lage der
geographischen Pole und den Erdradius möglich. Dieser war
offensichtlich geringer als der Heutige.
- Bringt
man die Kontinente in Ihre frühere Lage, so lassen sich
Gebirgszüge rekonstruieren, die eine Länge bis 2000
km
aufweisen und ein Alter zwischen 2 - 3,3 Milliarden Jahren besitzen.
Sie reichen über verschiedene Kontinente. Diese
Gebirgszüge
weisen eine äquatoriale Symmetrie bei einem Alter von 2,75 * 109
Jahren auf, wenn der Erdradius zu dieser Zeit 4400 km betrug. Ein
ähnliches Bild läßt sich auch aus
Altersbestimmungen
von Gesteinen mit einem Alter um 0,75 * 109 a
ziehen.
Zwischen diesen beiden Altern von Gebirgszügen liegt zwar
ebenfalls eine ausreichende Anzahl von Altersbestimmungen vor, die aber
keine Rückschlüsse auf den Erdradius gestatten.
Vorstehende
Angaben hat erstmals Dearnley (1965) in "Nature" beschrieben. Sie sind
von G. Sager (1976) zusammenfassend dargestellt worden.
- Untersuchungen
über die Häufigkeit und Verteilung maritimer
Sedimente auf
Kontinenten weisen darauf hin, daß seit dem Kambrium eine
Abnahme
der von Flachmeeren bedeckten Kontinentalflächen zu
verzeichnen
ist. Es gibt Annahmen, nach denen sich die Menge des Meerwassers eher
vergrößert als verringert hat. Dies
läßt den
Schluß zu, daß der Erdradius expandiert. Die
Expansion des
Erdradius soll in einem Bereich von 0,25 - 0,7 mm / a liegen Die
heutigen Kontinente, einschließlich der ihnen vorgelagerten
Kontinentalschelfe, können gut auf einem Globus von 3750 km
Radius
untergebracht werden. Wenn die Grenze der Schelfgebiete in ca. 200 m
unter NN angenommen wird, ist eine nahezu lückenlose Abdeckung
erreichbar und es bleiben nur schmale Rinnen, die nicht durch
Kontinentalflächen abgedeckt werden bzw. für die eine
doppelte Abdeckung erfolgt.
- Der Anteil der
Kontinentalschollen an der Erdoberfläche beträgt ca.
177 * 106 km2 . Wenn sich
die Erde in der Zeit seit der Bildung der Oberfläche vom Typ
der Kontinente (ca. 4,2 * 109
a) von 3750 auf 6371 km Radius ausdehnte, so stimmt die Summe der
heutigen Kontinentalflächen (einschließlich Schelfe)
in
ungefähr mit der damaligen gesamten Erdoberfläche
überein, wobei man zu einer pankontinentalen
Erdoberfläche
gelangt, welche vollständig oder zum Teil mit Flachmeeren
bedeckt
war. Aus dem heutigen Verhältnis von kontinentaler (alter) zu
maritimer (neuer) Erdoberfläche von 177 * 106
/ 333 * 106 km2
läßt sich eine Expansionsrate von 3,1 * 10-18
s-1 errechnen, wenn die Werte für
Erdradius, Radiusdifferenz und das zugehörige Alter in
Gleichung 4 eingesetzt werden.
- Auch
moderne Gravitationstheorien fordern z.T. eine Expansion von Objekten.
So gibt E.Schmutzer (2000) an, daß die 5-dimensionale
Projektive
Unified Field Theory für sphärische Körper
Expansion
fordert. Für den Erdradius wird ein Expansionswert von
Δr /
Δt =7,5 * 10-2 cm / y errechnet, was
einer Expansionsrate von 3,5 * 10-18 s-1
entspricht. Unter Bezug auf Treder gibt Lauterbach (1975) ebenfalls
eine Akzeleration von Orbitalgeschwindigkeiten bei Planeten und Monden
an, diese Akzeleration soll auf einer "Mach-Einstein-Doktrin" basieren.
Bereits in den 30er Jahren kommt P. Dirac, später P.Jordan
unter
Verwendung einer säkular abnehmenden Gravitationskonstante auf
eine Expansion der Erde. Die Rotationsverzögerung der Erde
kann
durch eine Expansion des Erdradius von ca. 0,06 cm / a erklärt
werden. Eine derartige Expansion kann jedoch nicht von den
Anhängern einer schnellen Expansion in Anspruch genommen
werden da
das Trägheitsmoment dies verbietet. Wenn die derzeitige
Rotationsverzögerung durch Gezeitenreibung zustande kommt, ist
derzeit eine Erdexpansion sehr wenig wahrscheinlich.
- Eine
Expansion der Erde ist anzunehmen, wenn das Universum mit der gleichen
Expansionsrate expandiert und die Hinweise auf kosmologische Expansion
in und außerhalb des Sonnensystems zu recht bestehen. Es gibt
Hinweise darauf, daß die kosmologische Expansion vorhanden
aber
imaginär ist. Das wäre dann auch für die
Erdexpansion
der Fall.
- Messungen
die mit Hilfe von VLBI und Satellitentechnik Ruder et.al (1990)
gewonnen wurden, verweisen auf eine Expansion der Erde.
- Neuere
Messergebnisse gestatten die Abschmelzung des Grönlandeises
und
den damit verbundenen Anstieg des Meeresspiegels abzuschätzen.
Dabei ist die Expansionsrate des Erdradius bis auf Meeresniveau gleich
der kosmologischen Expansionsrate. Das kann Zufall sein.
Merkwürdig daran ist, daß das nur für heute
gilt. Vor
100 Jahren war das ganz anders (Siehe Abschnitt 5).
- Entsprechend
Untersuchungen an hyperaktiven Galaxien des frühen Universums
sollten diese Galaxien expandiert sein. Entsprechend Abschnitt 16
dieser Arbeit ist die Expansionsrate gleich der Expansionsrate des
Universums. Das Verbot der kosmologischen Expansion in kleinen
Bereichen durch A. Einstein und E. G. Straus (1945) würde dann
weder für diese Galaxien noch für die Erde gelten.
Will
man die Expansionsrate der Erde errechnen und diese mit anderen Raten
vergleichen, so kann das geschehen indem man die Expansionsrate
α
aus dem Ausdehnungsfaktor des Erdradius pro Zeiteinheit wie folgt
errechnet:
Gleichung 4: r
= Erdradius [cm ], Δr
= Ausdehnungsfaktor [cm], t = Zeitraum (1 Jahr) [s],
α
=Expansionsrate
[s-1]
Gleichung 4.1
Das
Ergebnis stimmt in Phänomen, Dimension und Zahlenwert mit der
Hubblekonstante überein.
Auch
dann, wenn zusätzlich zu einer Erdexpansion eine
Gezeitenreibung
von maximal gleicher Größe (Retardationsrate
<
1*10-18 s-1) vorhanden
sein sollte, werden die
Toleranzen der Hubblerelation kaum überschritten. Geht man nun
infolge all dieser Hinweise, einschließlich der
verzögerten
Erdrotation davon aus, daß die Erde wirklich expandiert, so
ist
die scheinbar logische Folge, daß die Dichte der Erde
abnimmt.
Früher müßte auf alle Fälle die
Dichte der Erde
bei Expansion höher gewesen sein. Vor 4,3 * 109 Jahren,
einer Zeit für die man annehmen darf, daß die Erde
eine
feste Kruste ausgebildet hatte, die dann pankontinental war und
infolge ihrer Starrheit aufriß, war die durchschnittliche
Dichte dann aber ca. 17,3 gr / cm3.
Extrapoliert
man für die Entstehungszeit der Erde deren Radius, so kommt
man
auf eine zentrale Dichte, die noch wesentlich größer
war.
Mit Sicherheit kann man behaupten, daß die Erde nie ein
weißer
Zwerg war.
Die
extremen Dichtewerte in der Frühzeit unseres Planeten lassen
an
der Richtigkeit dessen Expansion zweifeln.
Bisher
wurden darum Effekte der Rotationsverzögerung der Erde mit der
Gezeitenreibung zu erklären versucht. Expansionseffekte wie
die
hier dargestellten wurden zur Kenntnis genommen und - ignoriert. Der
Autor neigt, besonders im Hinblick auf die noch folgenden Kapiteln,
zu der begründeten Meinung:
Alle
in dieser Arbeit beschriebenen Expansionseffekte mit einer Rate
um α ≈
2
- 3 * 10-18 s-1
sind vorhanden, aber
imaginär.
Eine
Lösung des Problems scheint sich abzuzeichnen, wenn die
Expansion der Erde durch Extrapolation über ihre
Entstehungszeit
hinaus weiter getrieben wird: Wäre die Erde vor einer Zeit
vorhanden, die man als Weltalter bezeichnet, so hätte sie
damals
eine Rotationszeit und einen Durchmesser „Null" besessen
und vor 10,7 Milliarden Jahren hätte ihr Radius und ihre
Rotationszeit ca. 20 % des heutigen Wertes betragen. Weiter unten mehr
dazu. Hinsichtlich der frühen extremen Dichtewerte sei auch
auf
Abschnitt
16 verwiesen,
wo offenbar gleiche Ursachen zu gleichen Ergebnissen
führen.
5.
Postglaziale Landhebung der Erde
Ruder,
Schneider und Soffel (1990) publizierten in Physikalische
Blätter 46 (1990) Nr. 2 den Aufsatz
„Geodäsie und
Physik“. Dort beschreiben sie Aufgaben und Ergebnisse des
Geodätischen Observatoriums Wettzell in Deutschland. Mit dem
damals neuen Ringlaser und dem Satelliten Lageos wurde genaueste
Messungen der Entfernung durchgeführt. Man erstellte ein
Multipolmoment der Masse der Erde. Daraus konnten
Größen
der kontinentalen Driftraten ermittelt werden. Diese Raten
können
mit paläomagnetischen Werten verglichen werden. Auch eine
wachsende Entfernung zwischen Nord- und Südpol von 1 mm / a
konnte ermittelt werden. Die zugehörige
Expansionsrate α
des polaren Erdradius ergibt
sich entsprechend Gleichung
4
aus der Radiusdifferenz pro Polradius und Jahr zu:
Gleichung
4: r
= Erdradius [cm ], Δr
= Ausdehnungsfaktor [cm], t = Zeitraum (1 Jahr) [s],
α
=Expansionsrate
[s-1]
Gleichung 5.1
Als
Ursache dieser Vergrößerung sieht man die Entlastung
vom
Eis der Eiszeit.
Die
Expansionsrate des polaren Erddurchmessers stimmt mit der
Expansionsrate des Universums überein.
Es
könnte zeitlich begrenzte Koinzidenz vorliegen. Die
korrespondierende Retardationsrate erhielt man zu 8 * 10-11
pro Jahr. Dieser
Wert wird hier umgerechnet pro Sekunde. Es ergibt sich 8 * 10-11
/ 31,56 * 106
= 2,5 * 10-18
s-1. Auch dieser Wert
entspricht der Expansionsrate des Universums. Die
Expansionsrate des Poldurchmessers ist, eine postglaziale
Dekompression als Ursache vorausgesetzt, zeitlich nur sehr begrenzt
von der angegebenen Größe, da das Abschmelzen der
Polvergletscherungen ein Vorgang ist der erst wenige Jahrtausende
zurückliegt. Wenn Hinweise aus anderen Erdformationen auf
Rotationsverzögerung existieren (z.B. Korallenkalender), so
muß
der Schluß auf eine Expansion des Erdpolradius im
obengenannten
Sinn falsch sein.
6.
Meeresspiegelanstieg durch Klimaänderung
Das
Onlinemagazin „Scinexx“
meldet am 04. Dezember 2009, daß ein Team der
Universitäten Stuttgart und Perth mit Hilfe des
Satelliten „GRACE"
festgestellt hat, daß das Grönlandeis abnimmt. Durch
genaue Bahnvermessung der Satelliten können
Gravitationsanomalien festgestellt und dann auf eine jährliche
Masseabnahme des Grönlandeises von 165 - 189 km3
geschlossen werden. Das entspricht einer
Vergrößerung des
„restlichen“ Geoids oder besser einem Anstieg des
Meeresspiegels von 0,5 mm / a. Das Geoid wächst also
entsprechend Gleichung
4
um eine
Rate
α
= 2,5.10-18
s-1
Gleichung 6
Die
Klimaerwärmung läßt die Entfernung des
Erdmittelpunktes vom Meeresspiegel durch das Abschmelzen des
Grönlandeises mit der Größe der
Hubblerelation
anwachsen.
Das
ist ein Wert, der zu Zweifeln keinen Anlaß gibt. Auch dann,
wenn die Aussage analog Abschnitt 5
ist und es sich nicht um eine
„Landhebung“ sondern
um eine „Meerhebung“ handelt. Es mutet trotzdem
seltsam
an, wenn man heute erstmalig eine derartige Messung
durchführen
kann die vor oder in 100 Jahren eine ganz
andere „unverdächtige“
Größe ergeben würde. Damals war ja die
Abschmelzmasse
geringer und der Anstieg des Meeresspiegels ebenfalls. Dazu kommt die
Koinzidenz zur postglazialen Landhebung.
7.
Der innere Erdkern
In
„Astronomische Nachrichten“ wird durch Denis
et.al. (2006) der Beitrag des inneren Erdkernes zur
Veränderung
der Länge des Tages und zur Rotation der Erde
erörtert.
Dabei kommt man zu der Annahme, daß der innere Erdkern
jünger
ist als die Erde. Sein Alter wird in den Grenzen von 1 - 3,5
Ga
(Mrd. Jahren) angenommen. Das entsprechende Wachstum erhält
man
zu 511,2 bis 146,1 km / Ga. Das entspricht für den oberen
Grenzwert des Alters einer Wachstumsrate:
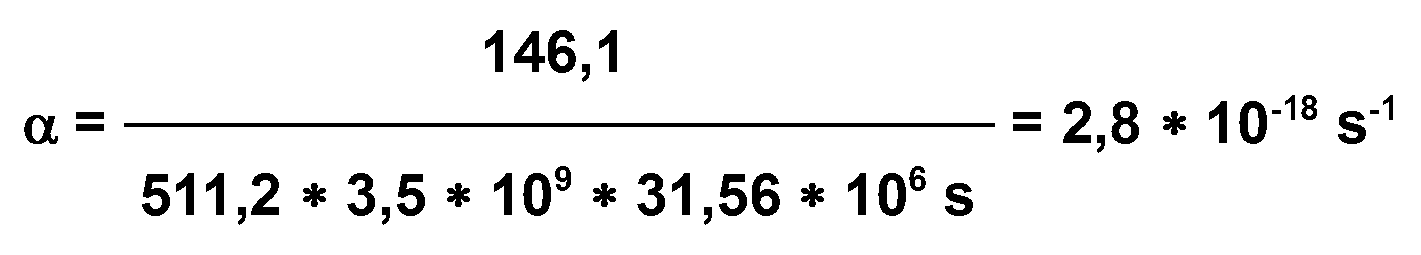
Gleichung 7.1
Der
untere Grenzwert ergibt immerhin noch eine Wachstumsrate von 1,28 * 10-17 s-1.
Übrigens
soll nach Angaben in dieser Arbeit bereits Runcorns
Hypothese von 1962 auf eine Bildung des Erdkerns mit
einem
durchschnittlichen Wachstum von 243 km / Ga führen. Das
entspricht einer Zunahme des Radius von 121,5 km / Ga und einer
Wachstumsrate von
Gleichung 7.2
Auch
wenn dieses Wachstum des Erdkernes durch gravitative oder chemische
Differenzierung oder anders erfolgt sein sollte, so beträgt
sein
Wert doch auf 19 Stellen genau dem Wachstum des Erdradius, wenn
dieses wegen der Rotationsverzögerung der Erde vorhanden sein
sollte. Sollte die Expansion des Erdradius nicht vorhanden sein, so
ergibt sich die Frage: Wieso ergibt sich für die, bei einem
fiktivem Erdradius von 3750 km zusammenpassenden Kontinentaltafeln
(Pankontinentale Erdkugel) und einem Alter von ca. 4,2 * 109
Jahren eine Expansionsrate von 3,1*10-18 s-1?
Natürlich
könnte man die Fragestellung
auch
umkehren: Wieso ergibt die Annahme dieser Expansionsrate der Erde ein
richtiges Alter für die Kontinente?
Wenn
der innere Erdkern, wie angeführt wächst, so ist die
Mindestwachstumsrate annähernd von der
Größe der
kosmologischen Expansionsrate.
Die
Übereinstimmung der vermuteten Expansionsrate des Erdradius
mit
der minimalen Expansionsrate des inneren Kernes ist als Hinweis auf
gleiche Ursachen zu werten.
8.
Erdoberfläche und Alter der Kontinente
Die heutigen
Kontinentalflächen, einschließlich der vorgelagerten
Kontinentalschelfe (ca. 177 * 106 km2),
können nach
Hilgenberg, Carey, Maxlow, Koziar, Vogel u.A. so auf einem Globus von
ca. 3750 km Radius untergebracht werden, daß eine nahezu
lückenlose Abdeckung dieses Globus mit
Kontinentalflächen
ohne Überlappungen und Fehlflächen erreichbar ist.
Das kann
nur als Expansion der früher kleineren Erde erklärt
werden. Deren (kontinentale) Oberfläche befand sich vielleicht
unter Wasser.
Stellt
man Gleichung
4
nach „t “
um so erhält man mit V.
Müller
(2009):
Gleichung 8
Setzt
man für Δr
den Wert ( 6371 - 3750 ) km , für r den
gegenwärtigen Erdradius und für α eine
Expansionsrate von 3,0 * 10-18
s-1
ein, so
erhält
man für die pankontinentale Erdoberfläche ohne Ozeane
für
das Alter einen Wert von ca. t = ca. 4,3 * 109
a. Bereits eine
geringe Abweichung von dieser Expansionsrate zeigt einen deutlich
falschen Wert für das Alter der kontinentalen Platten. So
würde
eine Expansionsrate a =
2,0 * 10-18 s-1
bereits
ein deutlich zu großes Alter von 6,52 Milliarden Jahren
ergeben. Die
Relation nach Gleichung 8 stellt somit ein sehr empfindliches
Instrumente zur
Bestimmung der Parameter dar. Der
Wert 3,0 * 10-18 s-1
entspricht
zwar nun nicht exakt dem Hubbleparameter es sollte jedoch beachtet
werden, daß auch andere hier relevante Werte (siehe
Tabelle am Schluß) zwar
in 18 Größenordnungen übereinstimmen aber
in der 19.
Stelle Differenzen auftreten. Ob diese Differenzen durch die
Gezeitenreibung, durch die Gravitationsfelder von Erde und Sonne oder
anders zustande kommen, soll hier nicht erörtert werden.
Natürlich
kann mittels Gleichung
4
auch
ein sicher bekanntes Alter der Kontinentalplatten zur Berechnung
einer Expansionsrate benutzt werden. Analog führt eine
Expansion
der Erde dazu, daß vor 4,3 Mrd. Jahren, also nach 0,686 des
heutigen Weltalters das Erdvolumen = 0,6863
=
0,323 und die Dichte = 3,096 des heutigen Wertes waren. Das sind ca. 17
gr / cm3 und
somit ist eine Erdexpansion aus dieser Sicht nicht akzeptabel. Analog
ist jedoch dann auch die Dichte der im Abschnitt 16 erwähnten
Galaxien nicht akzeptabel, obwohl diese Dichte
„gesehen“
wird.
9. Subduktion
Wenn
die Energie- und Massenbilanz der Erde ausgeglichen sind, so sollte
der Erdradius konstant sein. Von Effekten wie einer Abnahme der
Gravitationskonstante sei hier abgesehen. Wenn
also z.B. Magmamengen großen Umfangs (Flutbasalte) auf die
Oberfläche gelangen, so sollte sich dadurch der
durchschnittliche Erdradius längerfristig nicht
ändern. Die
oberflächlichen Massen werden sich im Laufe der Zeit der
irdischen Schwerkraft gehorchend so verteilen, daß der alte
Radius annähernd wieder erreicht wird. Zu beachten ist dabei,
daß die der Erde aufliegende neue Last das Innere der Erde
veranlaßt sich so umzuverteilen, daß die
Äquipotentialfläche der Gravitation
annähernd wieder
erreicht wird. (Dies gilt nicht, wenn die Gravitation geringer ist
als andere innere Kräfte, z.B. für kleine
Planetoiden). Für
die Erde ist bei Massenumverteilung keine Änderung der
sonstigen
globalen Parameter zu erwarten. Die Ausbreitung des Ozeanbodens an
den Mittelozeanischen Rücken führt nicht notwendig zu
einer
Vergrößerung des Erdradius. Eine Zunahme des
Volumens oder
der Masse der Erde hat jedoch eine Zunahme des Radius zur Folge. Massentransport
durch Erosion, der durch Flüsse weltweit erfolgt, wird von
Pfeufer
(2001) zusammenfassend
mit annähernd 10 km3 / a angegeben.
Bedenkt man, daß
die angeführten 10 km3 / a in 180 * 106
Jahren eine Sedimentmenge von 1,8 * 109 km3
bildet, so ist das gerade die Menge von Material, die in eben dieser
Zeit durch die Riftsysteme der mittelozeanischen Rücken zur
Ozeanbodenausbreitung beiträgt, wenn eine Stärke von
6 km
und eine neu gebildete Fläche von ca. 300 * 106
km2 dafür angesetzt
werden. Viele
Leute, die von der Expansion der Erde überzeugt sind nehmen
an, daß die ozeanischen Flächen den Zuwachs an
Erdoberfläche darstellen. Eine Subduktion sollte ihrer Ansicht
nach ausgeschlossen sein. Da das
sedimentierte Erosionsvolumen der Kontinentalfläche
annähernd
gleich groß ist, wie das extruierte Volumen,
müßte
das Sediment der letzten ca. 180 Millionen Jahre ebenso gut
nachweisbar sein, wie das aus dem Erdinneren ausgeschiedene Material
des Ozeanbodens. Natürlich kann das kontinentale
Erosionsvolumen
ebenso wie das marine Extrusionsvolumen aus dem Erdinneren
anteilmäßig zur Bildung des vorhandenen Ozeanbodens
beitragen.
Solange
das Verschwinden der kontinentalen Ablagerungen nicht bemerkt wird,
sollte das Verschwinden der annähernd gleich großen
Menge
an Extrusionsvolumen keine größere Bedeutung
erfahren.
10.
Urkilogramm
Rauner
(2003) gibt im Onlineportal „Die
Zeit“ an, daß
das Urkilogramm in den vergangenen 100 Jahren um 50 μg an Masse
verloren hat. Das entspricht einer Verlustrate von:
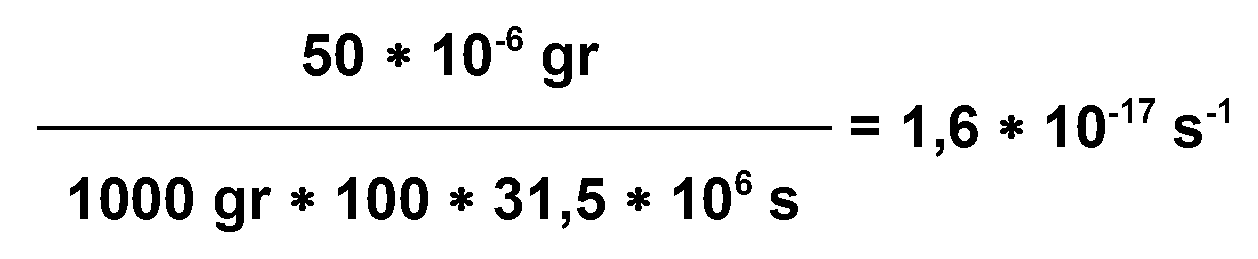
Gleichung 10
Diese Verlustrate ist ca. 5 mal
größer als
die Expansionsrate des Universums bzw. der Verzögerungsrate
der
Erdexpansion. Die
UT-Sekunde wird im Verhältnis zur SI-Sekunde immer
größer. Das
Sekundenpendel wird im Verhältnis zu Erdradius und
Universum (genau so, wie im Titel Südamerika) immer
kürzer.
Es muß also immer schneller pendeln. Das entspricht einer
Vergrößerung der Erdanziehung bzw. Erdmasse. Wenn
man nun auf der Definition des Kilogramms besteht, muß man
akzeptieren, daß die Erdmasse im Verhältnis zum
Urkilogramm immer größer wird.
Die
Masse des Urkilogramms wird also im Verhältnis zur Erdmasse
immer geringer.
Warum
sollte also der Erdradius (bei konstanter Dichte) nicht wachsen? Der
vom Autor im Vorwort geforderte Effekt, daß kleine
Gegenstände
nicht an der Expansion teilnehmen führt hier zu Ergebnissen,
die
die Frage nach der Massenkonstanz der Erde unter völlig
anderen
Gesichtspunkten erscheinen läßt.
Da
die Minderungsrate jedoch dem ca. 5fachen des Erwartungswertes
entspricht, ist diesem Argument keine zu hohe Bedeutung beizumessen
zumal das Meßverfahren und andere Randbedingungen nicht
bekannt
sind. Trotzdem ist eine Übereinstimmung mit der kosmologischen
Expansionsrate zumindest in der Größenordnung
gegeben. Der
Faktor 5 wäre z.B. durch eine "exzellente Griffigkeit
französischer Staubtücher" zu erklären. Es
wäre
jedoch auch möglich, daß früher die Erde
wirklich
(gegenüber kleinen Gegenständen) eine geringere
Masse
hatte und nur der "überhöhte Betrag" andere
Ursachen hatte. Dies führt, wenn man diesen
"Massenzuwachs" auch
anderen Weltkörpern zubilligt dazu, daß die heute
beobachteten Himmelskörper früher (wir beobachten
deren
frühere, geringere Masse) eine geringere Masse hatten. Diese
Masse fehlt wiederum den Kosmologen.
Eine
Änderung der Gravitationskonstante im Dirac'schen Sinn ist
für die allmähliche Vergrößerung
gravitationsdominierter Massen nicht erforderlich.
11.
Gezeitenreibung - Ursache der Rotationsverzögerung?
In der
Literatur wird im Wesentlichen die Gezeitenreibung für die
Rotationsverzögerung der Erde verantwortlich gemacht. Genaues
Zahlenmaterial, von der Ursache der Gezeitenreibung ausgehend, liegt
jedoch nicht vor. Rotationsverzögerung durch Gezeitenreibung
dürfte auch nicht über geologische Zeiträume
hinweg
konstant sein, da Veränderungen der Erdoberfläche und
die
Entfernung Erde - Mond angeblich eine wichtige Rolle spielen. Eine
einigermaßen konstante Bremsung der Rotation ist jedoch
infolge
der Anwendbarkeit von Gleichung
2.2
auf
sehr unterschiedliche Zeiträume anzunehmen. In diesen
Zeiträumen
traten aber erhebliche Veränderungen der
Erdoberfläche ein.
Erinnert sei hier an die Kontinental und Poldrift. Ebenfalls durch
die Gezeitenreibung soll die Vergrößerung des
Mondbahnradius durch Drehimpulstransfer zustande kommen. Der Mond
entfernt sich angeblich entsprechend seiner Entfernung exakt wie ein
extragalaktisches Objekt entsprechend dessen Entfernung von der Erde.
Dazu mehr im Abschnitt 12.
Dies
geschieht heute, vor tausenden von Jahren und vor 100 Millionen
Jahren genau so, wie vor 600 Millionen Jahren und, wenn man Dearnley
glauben will, schon vor 2,75 Milliarden Jahren, als auf der Erde der
Atlantik und der Indik noch gar nicht existierten und der Mond viel
näher stand! Trotz der gänzlichen
Veränderung der
Erdoberfläche und der Rückkopplung durch den
geringeren
Mondabstand sollte die Gezeitenreibung genau die
Rotationsverzögerung
bewirken, die nach Gleichung
2.2
relativ
konstant und von der Größe des Hubbleparameters sein
muß?
Die Übereinstimmung beträgt immerhin 18 (!)
Zehnerpotenzen, unabhängig vom genauen Wert und von der
zeitlichen Konstanz des Hubbleparameters.
Bereits
Kant hatte die Gezeitenreibung als mögliche Ursache einer
Rotationsverzögerung der Erde angenommen und Berechnungen dazu
angestellt. Er war davon ausgegangen, daß die Gravitation von
Sonne und Mond eine Strömung in den Ozeanen erzeugt, die
entgegen der Erdrotation verläuft und diese dadurch
verzögert. Den gleichen Mechanismus nimmt er für die
Herbeiführung der gebundenen Rotation des Mondes an. Er setzt
dabei voraus, daß sich der Mond noch "in flüssigem
Zustand" befand, als er die gebundene Rotation erreichte. Wenn
der Mond diesen Zustand jemals besaß, hätte er die
gebundene Rotation in bemerkenswert kurzer Zeit erreichen
müssen,
da die Proben des Mondgesteins auf ein Krustenalter von mehr als
3 * 109 Jahren schließen lassen.
Obwohl
die Parameter, welche die Gezeitenreibung verursachen auch heute noch
recht ungenau bekannt sind, ist man sich über die Existenz der
Gezeitenreibung im Wesentlichen einig. Auch der Autor
schließt
sich dieser Meinung an. Erst in den vergangenen 40 Jahren ergaben
sich Gesichtspunkte, welche die Gezeitenreibung für die
Erklärung der beobachteten Effekte nicht als ausreichend
erscheinen lassen. P.
Brosche und J. Sündermann (1969) geben
einen Wert der nur unter 40% des Beobachtungswertes erklären
kann. SAGER
(1976) vertritt
die Meinung, daß eine Expansionsrate des Radius der Mondbahn
von 4 * 10-18
s-1
(5
Meter in 100 Jahren) nicht mehr durch Gezeiteneinflüsse
bedingt
sein kann. Bei Bursa
(1985) ist
die Veränderung des orbitalen
Drehmomentes
2 Größenordnungen kleiner, als die
Gezeitendeformation der
Erde dies fordert.
Beider
Berechnung globaler Werte der Gezeitenreibung geht man davon aus,
daß
die Tideströme Vektoren darstellen und die
Reibungskräfte
Komponenten besitzen können, die sich beschleunigend oder
verzögernd auf die Erdrotation auswirken. Bei streng
harmonischen Tideströmen müßten sich beide
Komponenten gegenseitig aufheben. Man versucht nun in einem
möglichst
engmaschigen Gitternetz die Ozeane mit diesen Vektoren zu
überdecken. Unter enormen Aufwand ist es dann
möglich,
Werte
zu erhalten, die zwar tendenziell einer Gezeitenreibung entsprechen,
eine quantitative Sicherstellung dieser Werte ist jedoch heute noch
nicht im erforderlichen Umfang möglich. Anderseits kann eine
Abnahme der Rotationsenergie der Erde aus astronomischen
Beobachtungen recht genau zu - 3,6 * 1019
erg *
s-1 errechnet
werden. Dieser Wert deckt sich mit
den Werten
früherer erdgeschichtlicher Epochen, die aus den schon
erwähnten
fossilen Organismen errechenbar sind. Aus dem Vergleich zwischen den
aus Tidestrommessungen und aus astronomischen Messungen ermittelten
Werten, läßt sich im Prinzip die Frage beantworten,
ob die
Gezeitenreibung alleinige Ursache der Rotationsverzögerung
ist.
Solange ersterer Wert allerdings nicht genauer festliegt, kann
natürlich auch keine definitive Antwort erfolgen.
Es
gibt jedoch einen Umweg, um sich Klarheit über die
aufgeworfene
Frage zu verschaffen. Dabei kann auf die aufwendigen
Tidestrommessungen verzichtet werden. Dafür erhält
man auch
keinen Wert für die wirklich vorhandene Gezeitenreibung, wohl
aber einen maximalen Grenzwert, der sich mit den astronomischen
Messungen vergleichen läßt. Die Frage nach der
Gezeitenreibung besitzt für die Gesamtproblematik zwar keine
ausschlaggebende Bedeutung, jedoch einige Wichtigkeit. Es sei darum
hier versucht eine grobe Abschätzung dieses obigen
Grenzwertesfür die Gezeitenreibung zu erhalten. Bei dieser
Abschätzung wird davon ausgegangen, daß der
Gesamtdrehimpuls des Systems Erde-Mond bei einer
Rotationsverzögerung
der Erde erhalten bleiben muß. Auf die Verwendung maritimer
Parameter wird fastgänzlich verzichtet und es werden im
Wesentlichen theoretische Gesichtspunkte verwendet. Dieser Weg ist
gangbar, da nur eine theoretische obere Grenzgröße
benötigt wird.
Da,
wie erwähnt, bei Rotationsverzögerung der Erde der
Drehimpuls des Systems Erde-Mond konstant bleibt, muß sich
der
Drehimpuls (Bahnimpuls) des Mondes vergrößern.
Unsere
obige Frage wird also wie folgt abgewandelt:
Sind
die an der Gezeitenreibung beteiligten Massen in der Lage, gravitativ
die beobachtete Veränderung der Mondbahnelemente hervorzurufen?
Bei
Kenntnis dieser Massen ist es nun völlig unerheblich, ob ihre
Wirkung durch die innere Reibung des Wassers oder durch dessen
Bodenreibung zustande kommt. Es ist unwesentlich, wie groß
die
Vektoren der Tideströme sind und ob diese in den
Schelfgebieten
oder im tiefen Ozean wirken . Es bleibt sich gleich, wie
groß
die Tidenhübe sind, welche Massen in den einzelnen
geographischen Gebieten beteiligt sind. Es ist unerheblich welcher
Gezeitentyp vorliegt. Alle diese Parameter in denen die
Schwierigkeiten exakter Berechnungen liegen, werden
vernachlässigt
und es werden nur maximale Werte benutzt.
Welche
Parameter sollen nun für die Lösung der gestellten
Aufgabe
herangezogen werden?
Wir
gehen davon aus, daß der Mond durch seine Gravitation auf der
Erde zwei gegenüberliegende Flutberge erzeugt die in erster
Näherung bei den Kulminationspunkten der
Erdoberfläche
aufliegen. Infolge der, gegenüber dem Mondumlauf schnelleren
Erddrehung, werden diese Flutberge durch die hier
vernachlässigte
Reibung "mitgerissen". Die Amplitude dieser Flutberge, das
Hochwasser, wird dadurch nicht mit der Kulmination des Mondes
zusammen fallen und es entsteht ein gewisser Anstellwinkel β zwischen
der Kulminationslinie (Verbindungslinie Erdmittelpunkt -
Mondmittelpunkt ) und dem Hochwasser. Die Kulminationslinie teilt
infolge diesen Anstellwinkels jeden der beiden Flutberge in einen
größeren und einen kleineren Teil. Beide Teile haben
unterschiedliche Massen. Diese Differenzmasse jeden Flutberges wirkt
nun von ihrem Massenschwerpunkt aus gravitativ auf den Mond. Der
Massenschwerpunkt liegt gegen die Kulminationslinie um den
Winkel β
versetzt (siehe
Abb.
2). Alle
übrigen Wassermassen der Flutberge gleichen sich gegenseitig
aus
und sind deshalb ohne Belang. Die Differenzmasse des Flutberges bei
der oberen Kulmination wirkt durch ihre Gravitation beschleunigend
auf den Mond in seiner Bahn. Entsprechend wirkt die Differenzmasse
der unteren Kulmination verzögernd. Sollte nun durch
spezifische
Oberflächengegebenheiten der Erde die Differenzmasse bei der
oberen Kulmination größer sein als durchschnittlich,
so
ist das unerheblich, da sich nach 12 Stunden und 25 Minuten (1/2
Mondtag) ein ähnliches Bild bei der unteren Kulmination
aufbaut,
was im Durchschnitt zur Annullierung von Extremwerten führt.
Da
die Entfernung der Differenzmasse der oberen Kulmination zum Mond
geringer ist, als die der unteren Kulmination, ist die
Gravitationskraft der beschleunigenden Komponente auf den Mond
größer,
als die von der verzögernden Komponente ausgehende
Gravitationskraft. Dies führt zu einer Beschleunigung des
Mondes
in der Bahn, also zur Vergrößerung der Entfernung
Erde -
Mond. Dadurch entsteht eine Verspätung des Mondes
gegenüber
seinem vorberechneten Ort.
Soviel
zur Theorie der Gezeitenreibung bzw. des Drehimpulstransfers der
rotierenden Erde auf den Bahnimpuls des Mondes. Wie sieht nun die
quantitative Seite und ihre Erfassung aus?
Zu
beobachten ist eine Beschleunigung des Mondes von 10,4 Bogensekunden
in 100 Jahren. Diese setzt sich aus der Rotationsverzögerung
der
Erde (Beschleunigungsanteil 32,8") und aus der
Entfernungsvergrößerung des Mondes
(Verzögerungsanteil
22,4") zusammen.
Läßt
sich nun diese Verzögerung durch die Gezeitenreibung
begründen?
Für
eine Abschätzung der tatsächlich geleisteten
"Akzelerationsarbeit" durch die Gezeiten wird nun von
folgenden Annahmen ausgegangen:
- Das Hochwasser tritt
infolge der Gezeitenreibung durchschnittlich 30 Minuten nach der
Kulmination ein. Das entspricht einem Anstellwinkel von 7,5°.
Dieser Wert dürfte weit über dem
tatsächlichen liegen.
- Es handelt sich um
idealisierte Flutberge in Kegelform mit ca. 5000 km Radius und 53 cm
Höhe. Diese Höhe entspricht dem theoretisch zu
erwartenden mittleren Tidenhub.
- Die Differenzmassen
ergeben sich aus 1. und 2. zu ca. 2 * 1018 Gramm.
- Ihre Entfernung zum
Mond sei gleich der Entfernung Erdmittelpunkt -
Mondmittelpunkt
±
Erdradius.
Die
in diesen Punkten genannten Werte sollen nun dazu dienen, einen
Vergleich mit den Beobachtungswerten zu ermöglichen.
Die
Gravitationskräfte, welche durch die Differenzmassen auf den
Mond wirken, betragen in der oberen (F1) und in der unteren
(F2)
Kulmination:
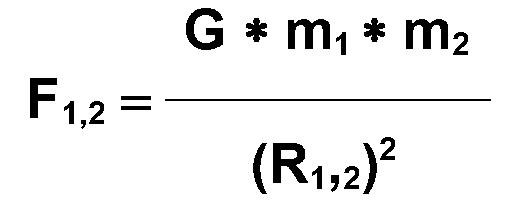
Gleichung
11: G
= Gravitationskonstante, m1
=
Differenzmasse eines Flutberges, m2
=
Masse des Mondes, R1,2
=
Abstand der Differenzmasse vom Mond in der oberen (R1)
und unteren (R2)
Kulmination
Nach
getrennter Berechnung der beiden Kräfte ist F1
entsprechend Abb. 3
mit dem Sinus des
Winkels
α1
und F2
mit sin
α2
zu
multiplizieren. Dadurch erhalten wir die Komponenten dieser
Kräfte,
die in der Richtung der Mondbahn wirken. Anschließend wird
die
Differenz gebildet und man erhält die resultierende
Kraft ΔF,
die
beschleunigend auf
den Mond wirkt. Unter Verwendung der Werte aus den Punkten 1 - 4
erhält man die Resultierende ΔF
= 2 * 1012
cm * gr * s-2. Wie bereits
erwähnt,legt der Mond in 100 Jahren gegenüber seinem
vorberechneten Ort eine Strecke von 22,4 Bogensekunden zurück.
Das entspricht inder Entfernung des Mondes einer Strecke von 42 km.
Diese Strecke multipliziert mit ΔF
ergibt ca. 8 * 1018
cm2
* gr * s-2. Dieser Wert ist
nicht
der
sich aus der Gezeitenreibung ergebende, sondern der in Unkenntnis der
Parameter mögliche Maximalwert. Zur Begründung des
Beobachtungswertes von 3,6 * 1019
cm2
* gr * s-2 ist dieser
Maximalwert noch zu klein.
Die
Expansionsrate der Mondbahn kann nicht allein durch Gezeitenreibung
verursacht sein.
Selbst
wenn nicht die Differenzmassen, sondern die gesamten Flutbergmassen
in die Rechnung eingehen, ändert das am Ergebnis kaum etwas
obwohl diese Annahme bereits unrealistisch ist. Die wirklichen Werte
dürften weit unter den hier angenommenen liegen. So wird z.B.
ein Anstellwinkel von b
=
7,5° zugrunde
gelegt während bei Zschau
(1978) für diesen Winkel (bei Festlandsgezeiten)
10-2
Grad angeben ist. Bei Verwendung dieses Anstellwinkels ergibt sich
ein Vergleichswert von ca. 1 * 10-13 cm2
* gr * s-2, also ein um viele
Größenordnungen kleinerer, als
der
obengenannte Beobachtungswert. Eine weitere
Vergrößerung
des Anstellwinkels über 7,5° hinaus ist nicht
sinnvoll. Es
nehmen dadurch die Differenzmassen noch etwas zu, dafür
muß
aber die Voraussetzung 4. fallen gelassen werden, was infolge der in
die Rechnung eingehenden Winkelfunktion für β →
90°
ein ΔF →
0 ergibt.
Falls
sich die vorstehenden Abschätzungen als richtig erweisen, so
kann die säkulare Expansion der Mondbahn von 3,8 cm pro Jahr
nicht durch Gezeitenreibung begründet werden.
Das
Ergebnis dieser Abschätzung deckt sich in seiner Aussage
tendenziell mit den Ergebnissen von Brosche
(1969), Bursa (1985) und Zschau (1978). Wieso
sich die Entfernung Erde - Mond vergrößert und die
Rotation der Erde sich verzögert dürfte somit als
offenes
Problem gelten. Es sei denn, man mißt der Weltzeitskala einen
tieferen Sinn bei.
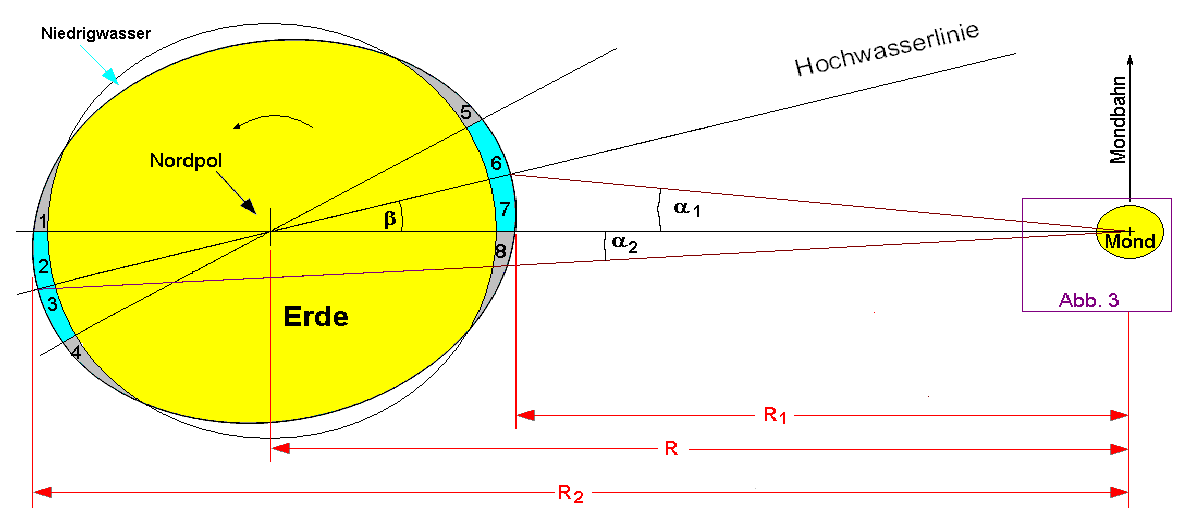
Abb.
2: Die zur Verbindungslinie Erde - Mond asymetrische Lage der
Differenzmassen (2, 3, 6, 7) und ihre gravitativen
Wirkungslinien (braun) auf den Mond
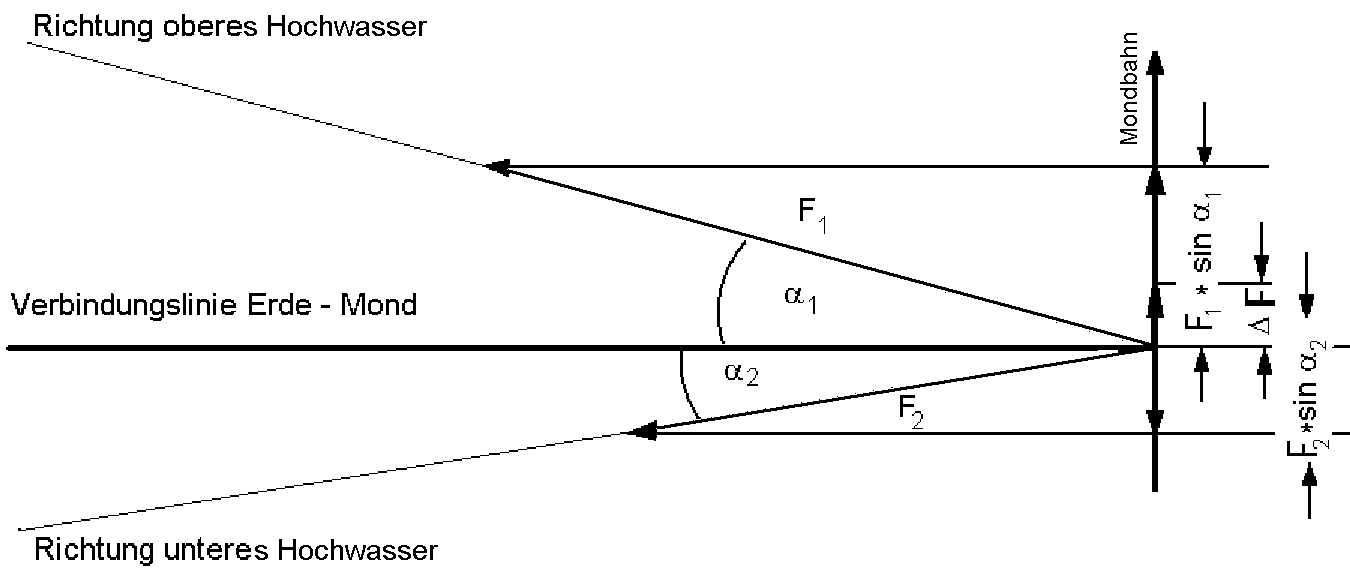
Abb. 3:
Durch irdische Gezeiten am Mond hervorgerufene Kräfte
Anzumerken
bleibt, daß eine Gezeitenreibung auch ausgeschlossen werden
muß, weil es weitere Indizien gibt, die gegen eine
Gezeitenreibung sprechen.
Ein
Beispiel:
Es
erscheint sehr verwunderlich, wenn eine zufällige
Übereinstimung
der Expansionsrate des Universums und Verzögerungsrate der
Erdrotation besteht. Wenn jedoch interplanetare Sonden mit
dergleichen 18-stelligen Rate verzögert werden, so potenziert
sich die Unwahrscheinlichkeit einer zufälligen
Übereinstimmung.
Siehe
auch V. Müller (2009)
12.
Die Expansion des Mondorbits
Der
Mond zeigt eine negative Beschleunigung in seiner Bahn. Wie im
Abschnitt über die Gezeitenreibung beschrieben, resultiert
diese
Verzögerung durch die Vergrößerung des
Mondorbits. Allgemein wird davon ausgegangen, daß das System
Erde - Mond ein konstantes Drehmoment hat. Da auch davon
ausgegangen wird, daß die Rotationsverzögerung der
Erde
durch Gezeitenreibung verursacht ist, wird der Drehimpuls, welcher
der Erde verloren geht auf den Mond übertragen. Die Art des
Transfers ist im Abschnitt 11
beschrieben. Die durch astronomische Beobachtung
gewonnenen
Werte der Verzögerung ergeben dann eine
Bahnvergrößerung
des Mondes. Inzwischen wurde auch mittels LLR-Technik eine
Vergrößerung des Mondbahnradius von
gegenwärtig ca.
3,82 ± 0,07 cm / Jahr (O.
J. Dickey et. al. 1994) gemessen. Dieser Betrag
ergibt mit Gleichung 4
eine Expansionsrate der Mondbahn von:
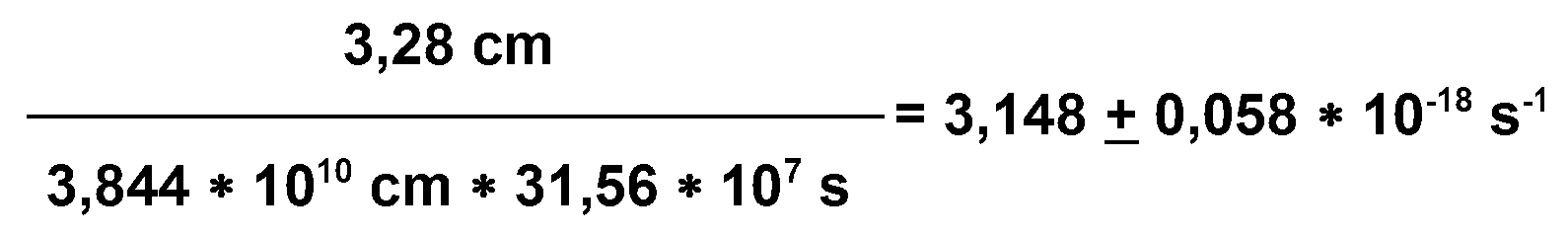
Gleichung 12
Die
Expansionsrate der Mondbahn ist annähernd von der
Größe
der Expansionsrate des Universums.
Der
leicht nach oben abweichende Wert könnte durch einen von der
Gezeitenreibung verursachten Anteil, aber auch vom Gravitationsfeld
von Sonne und Erde verursacht sein.
13.
Mars
Wenn
die Gezeitenreibung rotationsverzögernd auf die Erde wirkt,
dann
muß ihre Größe erdspezifisch sein.
Für Mars mit
seinen Kleinstmonden kann Gezeitenreibung praktisch ausgeschlossen
werden.
Eine
1952 erfolgte Reduktion der Rotationszeit des Mars ergab 24h 37'
22,6679",
worauf P.
Ahnert (1955) in
seinem "Kalender für Sternfreunde" hinweist. Dieser
und alle vorher erhaltenen Werte hatten nicht die SI-Sekunde, sondern
die variable UT-Sekunde zur Grundlage. Wäre die
Rotationsverzögerung der Erde durch Gezeitenreibung bzw.
innere
Ursachen zu begründen, so müßte eine,
gegenüber
der Erde beschleunigte Rotation des Mars zu beobachten sein.
Ältere
Messungen hatten ja kürzere UT-Sekunden benutzt. Der Vergleich
des bis 1952 allgemein akzeptierten Wertes von 1886 mit dem neueren
Wert widerspricht jedoch einer Rotationsbeschleunigung des Mars. Der
Mars unterliegt also offensichtlich einer Rotationsverzögerung
analog der Erde, die nicht durch Gezeitenreibung begründet
werden kann. Diese Verzögerung der Marsrotation stimmt
übrigens
wieder mit der von E.
Schmutzer (2000) geforderten
Marsexpansion gut überein.
14.
Die Pioneeranomalie
Die
beiden Sonden der NASA "Pioneer 10" und "Pioneer 11" wurden in den
Jahren 1972 / 73
gestartet. Da in größeren Abständen
Kontakt mit
ihnen hergestellt werden konnte, hat man festgestellt, daß
beide Sonden offensichtlich einer Kraft unterworfen sind, welche den
Sonden eine (negative) Beschleunigung erteilt, das heißt, sie
werden langsamer, als es entsprechend der Keplerbahn sein
sollte. Inzwischen ist ein ähnlicher Effekt auch für
die
Sonden "Ulysses" und "Voyager" gefunden worden. Trotz
gründlicher
Untersuchung mußten alle bekannten Ursachen für
die Verzögerung der Sonden ausgeschlossen werden. Die
Größe
der berechneten Verzögerung wird von J.
D. Anderson et. al. (2001) mit 8.74 ± 1.33 * 10-8
cm s-2 angegeben. Das
entspricht einer anormalen
Verringerung der Geschwindigkeit der Sonde von ca. 10 km/h in 100
Jahren. Betrachtet man nun nicht den Verzögerungswert |a|
sondern den durch die Lichtgeschwindigkeit dividierten Wert |a/c|, so
ergibt sich:
8,74 * 10-8
cm * s-2 = 2,92 * 10-18
s-1
*
299,792 * 108 cm * s-1
Gleichung 14
Die
Verzögerungsraten von Pioneersonden und Erdrotation sind
gleich.
Beide unterscheiden sich von der kosmologischen Expansionsrate nur
unwesentlich.
15.
Pulsare
Die
Pulsperiode von Pulsaren ist gleich ihrer Rotationszeit. Die
Pulsperiode unterliegt bei allen Pulsaren einer Verzögerung
was
einer Rotationsverzögerung entspricht. Die Ursache ist nach
allgemeiner Ansicht in der bremsenden Wirkung des mitrotierenden
Magnetfeldes oder in der Energieabstrahlung durch Gravitationswellen
zu suchen. Accretion und relativistische Effekte spielen ebenfalls
eine Rolle. Eine Expansion der Pulsare kann nicht ausgeschlossen
werden. Die Verzögerungsraten liegen liegen im Bereich 10-12
- 10-21 s-1. Nur
wenige Pulsare gestatten
die Messung ihrer Rotationsperiode und ihrer Verzögerungsrate
mit extremer Genauigkeit. Voraussetzung ist dabei, daß
Accretions- und Recyclingprozesse weitgehend ausgeschlossen sind und
relativistische Effekte ebenfalls nicht von erheblicher Bedeutung
sind. Die Meßgenauigkeit ist dann der Ganggenauigkeit von
Atomuhren ebenbürtig. Zu den bestuntersuchten Pulsaren
dürften
nachstehend aufgeführte gehören. Ihre hier
interessierenden
Elemente werden von Manchester,
R. N. et. al., (2005) im ATNF Pulsar Catalogue (Okt.
2005)
wie
folgt angegeben:
|
Name
|
Pulsperiode (s)
|
Verzögerungsrate
(s-1)
|
|
B 1913+16
|
0.0590299983444181
|
8.62713 E-18
|
|
B 1534+12
|
0.03790444080643456
|
2.4226281 E-18
|
|
B 2127+11C
|
0.0305292951283
|
4.99 E-18
|
|
B 1937+21
|
0.001557806472448817
|
1.051212 E-19
|
Die
Verzögerungsrate dieser hochpräzisen Messungen stimmt
relativ gut mit den Verzögerungsraten der Erde, der
Pioneersonden und den Expansionsraten von Mondbahn und Universum
überein. Für die Übereinstimmung der
Verzögerungsraten
der angeführten Pulsare ist somit die Expansion als Ursache
ebenfalls naheliegend.
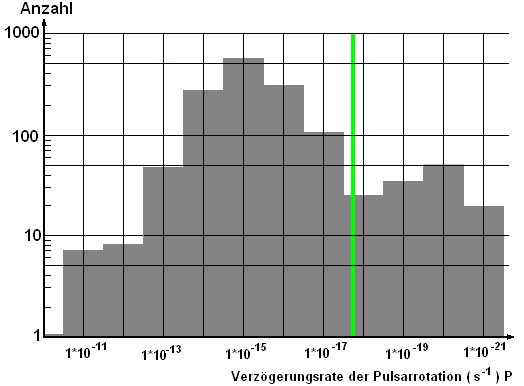
Abb.
4:
Verteilung von ca. 1500 Pulsaren auf die jeweiligen
Verzögerungsraten
der Pulsperioden. Bemerkenswert ist die Übereinstimmung einer
Extremstelle ( Minimum) des Kurvenverlaufs mit dem Wert des
Hubbleparameters (Grüne Säule).
Im
Diagramm läßt sich gut erkennen, daß bei
2,3 -
3,1 * 10-18 eine Extremstelle ist. Warum sich
dieses Minimum
ausgerechnet bei diesem Zahlenwert befindet ist nicht bekannt. Der
allgemein anerkannte Grund für die Verzögerungsraten
ist
eine Rotationsverzögerung dieser Objekte.
Die
bekannten 1500 Pulsare zeigen bei einer Verzögerungsrate von
der
Größe der kosmologischen Expansion eine Extremstelle
mit
unbekannter Ursache.
16.
Hyperaktive Galaxien des frühen Universums
Am
05. August 2009 gaben das Gemini-Observatorium und das HST eine
gemeinsame Pressemeldung heraus. ( www.gemini.edu/node/11303
)
Diese Meldung hieß: ASTRONOMERS FIND HYPERACTIVEGALAXIES IN
THE
EARLY UNIVERSE. In der Meldung wird mitgeteilt, daß das
Universum ein Alter von 3 Milliarden Jahren hatte, als das Licht der
von P. v. Dokkum
et. al. (2008) untersuchten
Galaxiengruppe emittiert wurde. Bei dem angegebenen Weltalter von
13,7 Mrd. Jahren ist das eine Entfernung von 10,7 Mrd. Lichtjahren.
Die Rotverschiebung beträgt nach M.
Kriek et al. (2009) z
= 2.1865. Die innere Dichte und Dynamik der beobachteten Galaxien ist
extrem. Die Masse muß im Bereich heutiger, großer
elliptischer Galaxien liegen. Im heutigen Universum existieren
derartige Objekte nicht. Galaxien solcher Masse sind im heutigen
(nahen) Universum 5 mal größer als im 3 Mrd. Jahre
alten
Universum. Es gibt offensichtlich keine andere Möglichkeit als
die, daß diese Galaxien seitdem expandieren. Ein Mechanismus
der Expansion ist nicht bekannt. V.
Müller
und M. Kokus (2010) gehen von einer kosmologischen Expansion aus. Die
genannten Angaben über die untersuchten Galaxien gestatten
eine
Berechnung der Expansionsraten. Zur Berechnung der Expansionsrate ist
die Größendifferenz pro Größe und
Zeit in
Relation zu setzen.
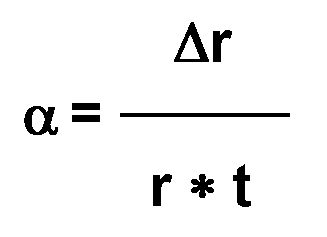
Gleichung
4: α = Erforderliche
Expansionsrate , Δr =
Differenz zwischen heutigem (5) und Emissionsradius (1), r
= adäquater, heutiger Radius (5), t = Entfernung in
Lichtlaufzeit
(SI-s)
Die
erforderliche Expansionsrate der untersuchten Objekte ist von der
Größe des Hubbleparameters.
Wir
sehen, daß die untersuchten Objekte vor langer Zeit
offensichtlich streng proportional die gleiche Expansionsrate
aufweisen, wie sie heute bei der Erde und im nahen Universum
vorliegt.
17.
Diskussion
Kosmologische
Folgen
Nimmt
man an, daß die Expansionseffekte mit der Rate um 2,5 * 10-18
s-1
eine gemeinsame Ursache haben, so kann diese Ursache nur kosmologischer
Natur sein. In diesem Fall findet eine Expansion des Raumes statt. Der
Raum selbst expandiert. Bei einer Expansion des Raumes bleiben
Durchmesser, Entfernungen und Dichte von Objekten im Raum trotz der
Expansion numerisch konstant. Die Lichtlaufzeiten bleiben im
expandierenden Raum ebenfalls numerisch konstant. Dabei ist es
unerheblich ob z.B. das Licht über den Durchmesser der
untersuchten hyperaktiven, frühen Galaxien zu einem
frühen
Zeitpunkt oder zu einem späteren Zeitpunkt auf der SI-Skala
läuft. Diese Aussagen sind dann sinnvoll und korrekt, wenn die
UT-Skala entsprechend Abschnitt 2 Verwendung findet und die
Expansionsrate konstant ist. Die Expansion der Objekte jedoch ist
imaginär. Distanzen sind numerisch konstant.
Die
Verwendung der SI-Sekunde führt dazu, daß nach 1/5
des
Weltalters die Durchmesser der Objekte 1/5 des heutigen Durchmessers
und ihr Volumen (1/5)3 bzw. ihre Dichte das
125fache des
heutigen Wertes betrugen. Analog führt eine Expansion der Erde
dazu, daß vor 4,3 Mrd. Jahren, also-von haute aus gesehen -
bei
einem Weltalter von 9,4 Mrd. (SI-)Jahren ( = 0,686 des heutigen
Weltalters) das Erdvolumen = 0,6863 = 0,323 und
die Dichte
= 3,096 des heutigen Wertes war. Das sind 17,09 gr / cm3 und
somit ist eine Erdexpansion unter dieser Sicht nicht akzeptabel. Die
Verwendung der UT-Skale ergibt jedoch ein Universum, welches eine
konstante Dichte und ein unbegrenztes Alter hat. Wenn
das nicht so wäre, und diese Galaxien expandieren in den
Raum,dann wäre die Expansionsgeschwindigkeit zwischen diesen
und
dem Beobachter eine Relativgeschwindigkeit. In diesem Fall ist nach
der Speziellen Relativitätstheorie zu verfahren und die
Lichtlaufzeit-Entfernung ist wie folgt zu korrigieren.
Δt = Δx *
u *
c-2
Gleichung
17.1: Δt
= Lichtlaufzeitkorrektur, Δx =
räumliche
Entfernungsänderung, u =
Radialgeschwindigkeit, c = Lichtgeschwindigkeit
Die
korrigierten Entfernungen entsprechen dann der UT-Metrik, das
heißt
die Lichtlaufzeiten verhalten sich wie bei Anwendung der UT-Metrik.
Dies führt bei Annäherung an den Grenzwert von 13,7 *
109
(SI-)Jahren
zu einem in der UT-Metrik in Raum und Zeit ebenfalls unbegrenztem
Universum.
Der
Wirkungsbereich der kosmologischen Rotverschiebung im Friedmann-Kosmos
In den
bisherigen Ausführungen wurde eine Reihe von
Beobachtungen, Messungen und Schlußfolgerungen behandelt, die
immer wieder auf eine Größe führen,
zumindest aber in
ihre nähere Umgebung. Bei dieser Größe
handelt es
sich um die gleiche, wie bei der Expansion des Universums. Alles dies
läßt einen kausalen Zusammenhang vermuten und das
stellt
die Kernaussage der vorliegenden Arbeit dar:
Die
Rotationsverzögerung der Erde ist Folge ihrer Expansion. Die
Expansion der Erde ist wesensgleich der kosmologischen Expansion.
Diese ist auf allen Größenskalen gravitativ
dominierter
Systeme nachweisbar.
Dieser
Vermutung widerspricht die 1945 von Einstein
und Straus (1945) gefundene Lösung der
Einsteinschen
Feldgleichungen. Danach existiert im expandierenden Universum um jede
Masse ein Bereich mit dem Radius Gleichung 17.2: 2M =
Schwarzschildradius der Masse,
r
= ( 6M / æ
µ
c2)1/3
Gleichung 17.2: 2M =
Schwarzschildradius der Masse, µ = Substratdichte im
Universum (3 * 10-31
gr / cm3), c = Lichtgeschwindigkeit, æ = Einsteinsche
Gravitationskonstante (2 * 10-48 gr-1
cm * s2)
In
diesem Bereich ist die kosmologische Expansion ausgeschlossen.
Für
die Erde ist dieser Bereich von einem Radius der
Größenordnung
1019 cm (
≈
10 Lj.).
Das
heißt:
Eine
Expansion der Erde und ihre verzögerte Rotation kann im
Friedmann-Kosmos ursächlich nicht von der kosmologischen
Expansion hergeleitet werden.
Weiterhin
ergibt sich aus dieser Arbeit, daß zwischen den einzelnen
Objekten gravitativ gebundener Systeme (Nebelgruppen und
-haufen) keine kosmologische Rotverschiebung existiert und diese
Systeme keine kosmologische Expansion erfahren. Der Radius dieser
Schwarzschild-Vakuole, in dem die kosmologische Expansion nicht
wirksam sein soll, ergibt sich daraus, daß die
durchschnittliche Substratdichte im Zentralkörper der Vakuole
konzentriert ist und bei Einhaltung der durchschnittlichen
Substratdichte dessen Umgebung praktisch materiefrei ist. Bei den
obigen Ausführungen über den Wirkungsbereich der
kosmologischen Expansion wurde auf nachfolgende Zusammenhänge
noch nicht eingegangen. Entsprechend
der Allgemeinen Relativitätstheorie sind zur Messung von
Eigenzeitintervallen punktförmige Uhren zu verwenden. Das
trifft
besonders für die Frühzeit des Universums zu, wo zur
Zeitmessung nur Umwandlungsprozesse der Elementarteilchen in Betracht
kommen. Dabei ist selbst in unmittelbarer Nähe der
Singularität, gemessen in der Zahl der ablaufenden
physikalischen
Einzelprozesse der "Weltanfang" noch sehr bzw. unendlich
weit entfernt (siehe
H.
Stephani
(1977)). Das bedeutet, daß bei
Annäherung an die
Singularität die Eigenzeitintervalle immer kürzer
werden
und gegen Null gehen. Dem gleichen Phänomen begegneten wir
bereits im 2.
Abschnitt
in Bezug auf die UT-Skala. Entsprechend der Beziehung Gleichung
2.1
bzw. Gleichung 2.2 werden mit wachsender Vergangenheit
die
UT-Sekunden gegenüber den SI-Sekunden kürzer und
gehen
gegen Null. Seit der kosmologischen Singularität sind
unendlich
viele UT-Sekunden vergangen. Berücksichtigt man nur die
säkulare
Akzeleration aus Gleichung
2.2
und
verzichtet auf alle anderen genauen Zeitkorrekturen, so hat man mit
dieser UT-Skala ein Zeitmaß welches mit höchster
Genauigkeit den Ablauf der Eigenzeitskala der Erde
repräsentiert.
Die
UT-Skala ist mit der Eigenzeitskala eines Objektes identisch. Nicht
die Rotation der Erde bestimmt den Ablauf der UT-Zeit sondern
umgekehrt.
Früher
war die UT-Sekunde gegenüber der für das Jahr
1900 definierten ET-Sekunde kürzer. Jedem Zeitpunkt der
UT-Skala
läßt sich ein Längenmaß zuordnen.
Entfernungen
können als Funktion der zeitlichen Distanz angesehen werden. Ordnet
man nun in der UT-Skala eine Entfernung zu, so wird das
räumliche
(UT-)Maß um so kürzer, je früher ein
Zeitpunkt
aufder SI-Skala festgelegt ist. Zum Zeitpunkt einer früheren
Emission eines Signals war auch das Zentimeter kürzer.
Für
die Erde bedeutet das, daß sie trotz ihrer Expansion in
dieser
Metrik einen konstanten Radius und konstante Dichte hat. Von einer
konstanten Rotationszeit (86400 UT-Sekunden) war bereits im Abschnitt
2 ausgegangen worden.
Die
Erde expandiert mit dem Raum, nicht in den Raum! Rotationszeit,
Volumen und Dichte sind darum konstant.
Einen
konstanten (UT-)Radius und konstante (UT-)Dichte haben auch die im
Abschnitt 16
genannten
„Hyperaktiven“ Galaxien.
Die
in der SI-Metrik beobachtete Expansion der Erde ist der Ausdruck
dafür, daß sie nicht die innere mechanische
Festigkeit
besitzt, der Expansion des Raumes zu widerstehen. Die
Gravitationskräfte sind im betrachteten Bereich
stärker als
andere Grundkräfte.
Die
Erde wird von der Gravitation dominiert.
Die
kosmologische Expansion kann somit proportional der betrachteten
Entfernung bis in "irdische" Größenbereiche
wirken und zwar offensichtlich bis hin zur Grenze von Bereichen, in
denen die Gravitation ihre Dominanz verliert. Bis zu der Grenze, wo
Kristall- und Molekularstrukturen der Gravitation widerstehen. Bis in
jenen Bereich, in dem andere Felder als die Gravitation dominieren. In
diesem Bereich können die gravitativ hervorgerufenen Effekte
infolge ihrer dort untergeordneten Rolle nicht in Erscheinung
treten. Die Struktur des Raumes wird in hinreichend kleinen Bereichen
unerheblich. Die obere Grenze dieser Bereiche dürfte an der
Begrenzung jeweils noch fester Körper liegen.
Brückenbauwerke
z.B. gehorchen der Struktur des Raumes erst dann, wenn bei Belastung
die gravitativen Kräfte größer als die
molekularen
werden. Wenn feste Gegenstände zu massereich sind, reichen die
Molekularkräfte nicht mehr aus der Gravitation zu
widerstehen. Für die Erde resultiert die annähernde
Form
eines Rotationsellipsoids. Die elektromagnetischen (molekularen)
Kräfte kleiner Planetoiden sind offensichtlich
größer
als deren Gravitationskräfte. Sie haben aus diesem Grund
unregelmäßige Formen, die nicht von der Schwerkraft
geprägt sind. Kontinentalschollen sind zu groß, um
bei
Expansion des Erdradius Stand zu halten. Die kontinentale Kruste der
ehemals kleineren Erde riß auf und zerbrach später
in die
heutigen Kontinente. Diese werden vorläufig weiter zerbrechen
wie z.B. heute Afrika und die pazifischen Geoplatten. Feste
Gegenstände der Umgebung werden dagegen keine Expansion
zeigen.
Ein konstantes Meerwasservolumen könnte jedoch expandieren. Widerspricht
das nun nicht der am Anfang dieses Kapitels gemachten
Feststellung, daß eine kosmologische Expansion der Erde im
Friedmann-Kosmos nicht möglich ist? Keineswegs! Es mag zwar
verwundern, daß man hier zu einem Ergebnis gelangt, welches
scheinbar im Widerspruch zu der eingangs gemachten Feststellung steht
und daß die kosmologische Expansion bis in wesentlich
kleinere
Bereiche zuläßt. Dieser Widerspruch ist jedoch nur
scheinbar. Die Beziehung in
Gleichung
17.2
gilt nur in einem Friedmann-Kosmos mit
Robertson-Walker-Metrik
und nicht in einem Universum, das seinen Anfang vor unbegrenzt vielen
(UT-)Sekunden nahm und das sich räumlich unendlich weit
erstreckt.
Dieses
ist kein Friedmann-Kosmos !
Nach
Ansicht des Autors läßt sich unter dieser
Betrachtungsweise ein kosmologisches Modell widerspruchsfrei
aufbauen, welches nicht dem Standardmodell des Urknalls
entspricht, diesem Modell aber auch nicht widerspricht, da es nicht
dessen gleichförmig ablaufende ET-Skale zur Grundlage hat.
Inwiefern die Zeit unter gegebenen physikalischen Bedingungen streng
gleichförmig ablaufen kann, sei offen gelassen. Ist nicht
das „Weltalter" ein gleicher Grenzwert, wie die
Lichtgeschwindigkeit und seine Überschreitung ebenso sinnlos?
Dürfen wir ein absolutes Maß, eben die SI-Sekunde, bis
in die Nähe dieses Grenzwertes überhaupt anwenden?
Für
hyperaktive Frühtypgalaxien führt die Anwendung der
SI-Metrik zu scheinbaren Widersinnigkeiten. Bei Anwendung der
UT-Metrik treten diese nicht auf.
Deswegen
scheint es angebracht die UT-Skala als kosmologisch sinnvoll
anzusehen. Auch Probleme, die in Zusammenhang mit der Expansion der
Erde und deren früher überhöhten Dichte zu
sehen sind,
entfallen.
Die
3°K-Strahlung
Identifiziert
man die Weltzeitskale (UT) auf Grund der Beobachtungen mit der im
Universum verwirklichten Zeitskale, so hat dieses keinen zeitlichen
Anfang bzw. ein unbegrenztes Alter. Seine räumliche
Erstreckung
ist gleichfalls unbegrenzt. (In den bisherigen ca. 14 * 109
(SI-)Jahren sind unendlich viele
UT-Sekunden
vergangen.) In einem solchen Universum sollte das fotometrische
Paradoxon nach Olbers, zumindest aber in modifizierter Form
erfüllt
sein. Das heißt, jeder Punkt der Sphäre sollte mit
einem
Objekt besetzt sein, wenn das kosmologische Prinzip gilt. Nach Olbers
sollte die Sphäre mit "Sonnenhelligkeit" strahlen.
Geht
man von der Durchschnittstemperatur von ca. 3000 °K bei z
≈
1000 aus, so
ergibt sich:
-
Wir befinden uns im Zentrum eines hohlen Raumes, der von
außen
mit einer Sphärentemperatur von 3000 K strahlt.
-
Unsere Umgebung wird dadurch auf die Temperatur der empfangenen
Strahlung aufgeheizt.
-
Der Charakter der schwarzen Strahlung (Hohlraumstrahlung) ist damit
gegeben.
-
Bei der kosmologischen Rotverschiebung dieser Strahlung von z
≈
1000 hat
deren Temperatur bei uns
3 °K erreicht.
Im
expandierenden Universum beträgt die scheinbare Helligkeit
eines
Objektes:
Gleichung
17.3: l
=
scheinbare Helligkeit, L
=
absolute Helligkeit,
r
=
Distanz, z
=
Rotverschiebungsfaktor
Die
Faktoren 4 π
r2
ergeben
sich aus der Ausbreitung des Lichte auf die Kugelfläche und (1
+
z)2 aus
dem Energieeffekt einerseits und dem Verdünnungseffekt
anderseits. Liegt jedoch keine Radialgeschwindigkeit vor, so
entfällt
der Verdünnungseffekt und aus Gleichung
17.3
wird:
Gleichung
17.4
Da
die Rotverschiebung z
≈
1000
gesetzt ist, ergibt sich aus den Gleichungen
17.3
und 17.4, daß
der Strahlungsfluß 103
mal und die
Energiedichte 109
mal höher
anzusetzen sind als beim Vorliegen einer Radialgeschwindigkeit. Da
die Energie eines Quants der 3°K-Strahlung den 1012ten Teil der
Energie
eines Baryons entspricht, ist das Verhältnis der
Energiedichten
von 109 /
1012 gegeben.
Dieses Verhältnis entspricht den Beobachtungswerten. Das nach
vorstehenden Ausführungen zu erwartende fotometrische
Paradoxon
nach Olbers ist somit in Form der 3°K-Strahlung
erfüllt.
Die
Sphäre über uns ist "sonnenhell" aber extrem
rotverschoben.
Die
Sphäre ist jedoch nicht unbedingt mit Sternen besetzt sondern
mit Materie schlechthin. Übrigens
ist
auch im expandierenden Standarduniversum jeder Punkt der
Sphäre
besetzt und strahlt mit ca. 3000 °K.
18.
Zusammenfassung
/ Summary
Es
gibt eine Reihe von Werten die genau oder annähernd mit der
Expansionsrate des Universums übereinstimmen. Diese Werte gibt
es in allen Größenbereichen, in welchen die
Gravitation
dominiert. Eine
zufällige Übereinstimmung dieser Werte ist abwegig. Das
bedeutet,
die
angeführten Phänomene besitzen die gleiche Ursache. Eine
evtl. Expansion des Universums fordert also auch Expansion von Erde,
Mondorbit, Frühtypgalaxien usw. Die
hier errechneten Werte sind zum Teil nicht anders begründbar,
als durch (kosmologische) Expansion. Eine
kosmologische Expansion ist nur dann gerechtfertigt, wenn die
SI-Metrik Verwendung findet. Mehrere
Phänomene weisen darauf hin, daß für die
gemessenen
Parameter wie Dichte, Dynamik, Geschwindigkeit die Eigenzeit und
nicht die SI-Zeit maßgeblich ist. Die
von uns vermessbare Eigenzeit ist mit der UT-Zeit identisch. In
der UT-Metrik gibt es keine kosmologische Expansion und keinen
Urknall. In
dieser Metrik ist das Universum unendlich in Raum und Zeit. Ein
Verbot der Expansion in kleinen Bereichen im Sinne von Einstein /
Straus gibt es nicht.
Thereare
some values which agree exactly or roughly with the expansion rate of
the universe. Thesevalues
are found in all size ranges in which the gravity is dominant. An
accidental correspondence of these values is impossible. The
means, the quoted phenomenons possess the same cause. Anexpansion
of the universe demands also expansion of earth, lunar orbit, early
galaxies etc. Thevalues
calculated here are not partly differently foundable as by
(cosmological) expansion. Acosmological
expansion is justified only if the SI metrics finds use. Severalphenomena
point out to the fact that for the measurable parametreslike density,
dynamism, speed the proper- time and not the SI-time is decisive. Theroughly
proper-time measurable from us is identical with the UT time. In
the UT metrics there is no cosmological expansion and no big bang. In
this metrics the universe is endlessly in space and time. Thereis
not a ban of the cosmological expansion in small areas in the mind of
Einstein/Straus.
Zusammenstellung
relevanter Werte
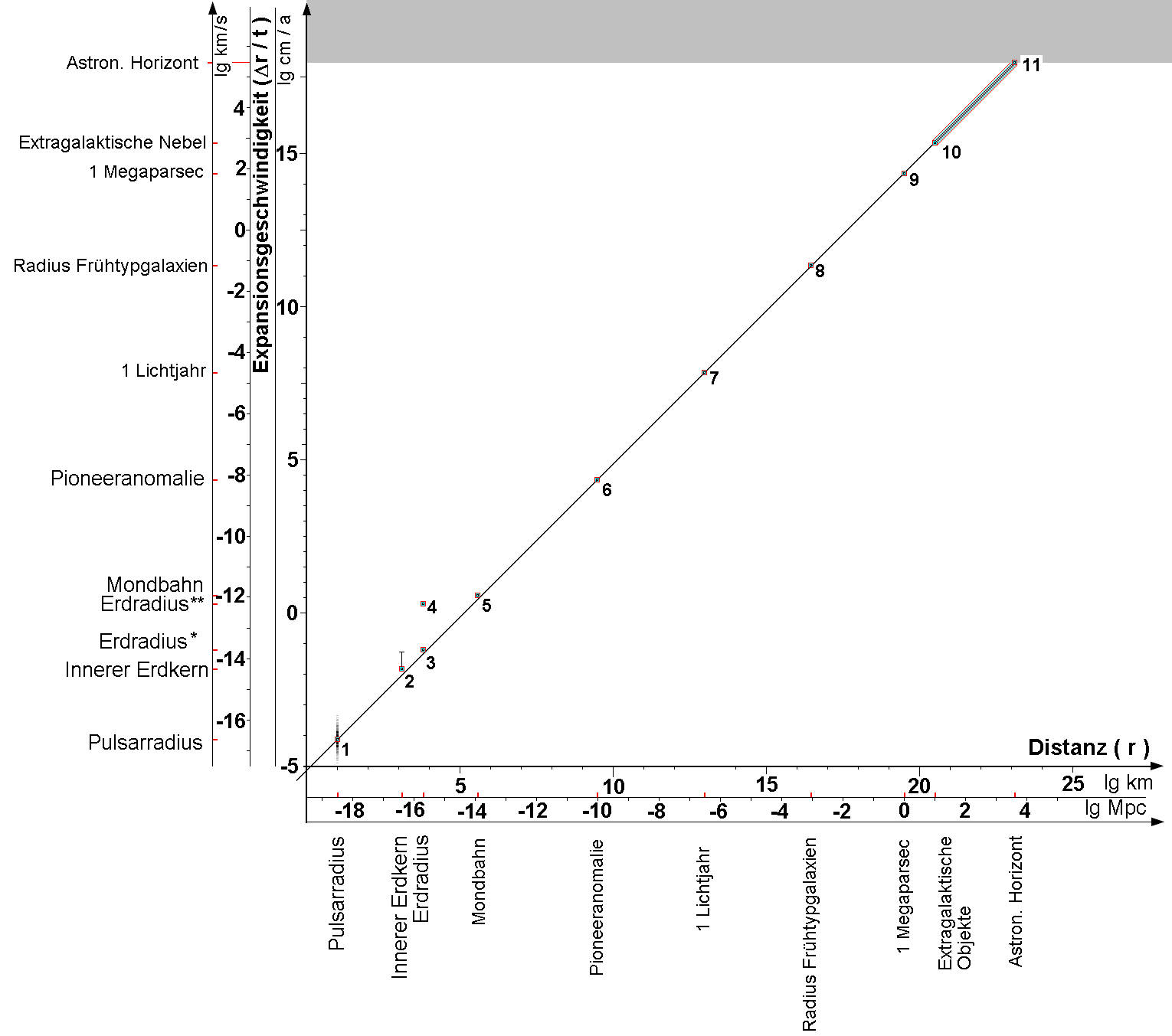
Abb, 5: Diagramm
zur proportionalen Beziehung zwischen Entfernung und
Expansionsgeschwindigkeit
Im
vorstehenden Diagramm verwendete Werte
| 1 |
2 |
3 |
4 |
5 |
6 |
| 11 |
Astronomischer Horizont |
1,265
* 1023
km |
lg
23.10 |
299805
km s-1 |
lg
5.48 |
| 10 |
Extragalaktische Objekte |
>3
* 1020
km |
lg
20.48 |
>700 km s-1 |
lg 2.85 |
| 9 |
1
Mpc |
3,087
* 1019
km |
lg
19.49 |
71
km s-1 |
lg
1.85 |
| 8 |
Radius
von Früh-Typ-Galaxien |
2,778
* 1016 km |
lg
16.44 |
0,07
km s-1 |
lg
-1.15 |
| 7 |
1
Lichtjahr |
9,46.1012
km |
lg
12.98 |
2,24.10-5
km s-1 |
lg
-4.65 |
| 6 |
Pioneeranomalie |
3
* 109
km |
lg
9.477 |
22436
cm a-1 |
lg
4.35 |
| 5 |
Mondbahn |
384600
km |
lg
5.585 |
3,8
cm a-1 |
lg
0.58 |
| 4 |
Erdradius
** |
6371
km |
lg
3.804 |
2
cm a-1 |
lg
0.30 |
| 3 |
Erdradius
* |
6371
km |
lg
3.804 |
0,06
cm a-1 |
lg
-1.21 |
| 2 |
Innerer
Erdkern |
1222
km |
lg
3.087 |
≥ 0,0146 cm a-1 |
lg
-1.835 |
| 1 |
Radius
der Pulsare |
10
km |
lg
1.000 |
7,64.10-5
cm a-1 |
lg
-4.12 |
Spalte:
1
= Nummer des Diagrammpunktes
2
= Phänomen
3
= Distanz in km
4
= Logarithmus der Distanz
5
= Expansionsgeschwindigkeit
6
= Logarithmus zu Spalte 5
Fußnote:
*
Expansionsgeschwindigkeit
aus der Verzögerungsrate bei konstantem
Trägheitsmoment der
Erde .
**
Expansionsgeschwindigkeit entsprechend
der Annahme von Carey, Maxlow, Koziar und Anderen zum Vergleich
Relevante
Expansions- und Verzögerungsraten
| Kriterium |
Rate
(n * 10-18 s-1)
|
Allgemein
akzeptierte
Ursache |
Fundstelle
zur kalkulierten Rate |
Fundstelle
obiger Abschnitt |
| Angleichung
ET - UT |
3,01
bzw. 2,93 |
Gezeitenreibung |
Ahnert,
1959 |
2 |
| Mondbahnexpansion
LLR-Messung |
3,15 ±
0,06 |
Gezeitenreibung |
Ruder,
1990 |
12 |
| Flächenverhältnis
Ozeane / Kontinente |
3,03 |
Unbekannt
(Hypoth.Erdexpansion) |
Müller,
2009 |
4 |
| Fossilien
Kreide - Kambrium |
4,1
-
3,01 |
Gezeitenreibung |
|
|
| Alte
irdische Faltengebirge (2,75 Mrd a) |
3,57 |
Unbekannt
(Hypoth.Erdexpansion) |
Sager,
1976 |
4 |
| Postglazialer
Poldurchmesser der Erde |
2,5 ±
0,95 |
Entlastungshebung |
Ruder,
1990 |
5 |
| Alter
der Kontinente |
3 |
Unbekannt
(Hypoth.Erdexpansion) |
|
8 |
| Meeresspiegelanstieg |
2,5 |
Klimaerwärmung |
|
6 |
| Hubblerelation
Vaucouleurs 1982 |
3,08 |
Kosmologische
Expansion |
|
|
| WMAP |
2,30 ±
0,26 |
Kosmologische
Expansion |
|
|
| Sonnensystem
/ Pioneeranomalie |
2,91 ±
0,44 |
Unbekannt |
Anderson,
2001 |
14 |
| Verzögerungsrate
PSR 1534+12 |
2,4 |
Massenverlust |
Manchester,
2005 |
15 |
| Wachstumsrate
von Früh-Typ-Galaxien |
2,37 |
Unbekannt |
v.
Dokkum, 2008 |
16 |
| Wachstumsrate
innerer Erdkern |
12,8
- 2,6 |
Phasenwandlung |
Denis,
2006 |
7 |
| Verlustrate
Urkilogramm |
16 |
Unbekannt |
Rauner,
2003 |
10 |
| ProjektiveEinheitl.Feldtheorie/Erdexpansion |
3,57 |
Skalare
Expansion |
Schmutzer,
2000 |
|
Spekulative
Zusammenhänge
| Im
Maßsystem |
ergeben
Messungen von gravitativ dominierten Körpern |
ergeben
Messungen von Körpern und Bereichen, die durch andere
Grundkräfte domoniert sind |
| SI-System |
Expansion |
Konstanz |
| UT-System |
Konstanz |
Kontraktion |
| Beispiele |
Radius
sphärischer Körper (Erde), Lichtzeit zu kosmischen
Objekten, Rotationszeit von Erde, Mars und Pulsaren |
Elektromagnetische
Wellenlängen,
starre Körper, Urmeter, Sekundenpendel |
Literatur
Ahnert,
P., (1959), Kalender für Sternfreunde 1959 S 92 J. A. Barth
Verlag Leipzig
Ahnert,
P., (1955), Kalender für Sternfreunde 1955 S 92
J. A.
Barth Verlag Leipzig
Anderson,
J. D. et al., 2001. Studyof
the anomalous acceleration of Pioneer 10 and 11. ar Xiv: gr-qc/0104064
Bär
(2008) http://
www.nabkal.de/akzel.html
Brosche,
P., Sündermann, J.,(1969), Erdrotation und
Gezeitenreibung. Mitt. Astron. Ges. 27, 131 1969
Bursa,
M., (1986), Variations in the Moon's due to Earth's
tides.
Bull. Astron. Inst. Czechosl.37 (1986), 80 - 84
Carey,
S. W., (1996), Earth Universe Cosmos, Chapter 7 Earth
Expansion On-line books and papers regarding global expansion
tectonics
Denis,
C. et.al., (2006), Secular
changes of LOD associated with a growth of the inner core in: Astron.
Nachr. 327,
No.4 ,
309-313 (2006)
Dearnley,
R., (1965), „Orogenic fold-belts, convections
and
expansion of the earth“ Nature 206 / 1965
Dickey,
J. O. et al., 1994. Lunar laser ranging: A continuing
legacy
of the Apollo program. Science, 265, 482-490
v.
Dokkum, P. et al., 2008 “Confirmationof
the remarkable compactness of massive quiescent galaxies at
z~2.3,”
Astrophysical Journal, 677:L5 - L8
Egyed, L., (1969) Physik der Erde.
German
translation of: A Föld Fizikája)
Akadémiai Kiadó,
Budapest 1969
Einstein,
A. und Straus, E. G., (1945),
Rev. Mod. Phys. 17, 120 (1945)
Hilgenberg,
O. C. (1933), „Vom wachsenden Erdball“ Berlin 1933
Kriek,
M. et al., (2009), An
Ultra-DeepNear-Infrared Spectrum of a Compact Quiescent Galaxy at
z=2.2 http://a
rXiv.org/pdf/0905.1692v2
Lauterbach,
R., (1975), Physik
des Planeten Erde, Berlin. Akademie-Verlag. 1975
Manchester,
R. N. et.al., (2005), The
ATNF Pulsar Database.
http://www.atnf.csiro.au/research/pulsar/psrcat/
Müller,
V., (2009), Doescosmological
expansion exist on smaller scale? NCGT Newsletter Issue 50 P. 18 - 22
Müller,
V. und Kokus, M., (2010), „HighMass
and High Redshift Elliptical Galaxies and Interpretations of
Hubble’s
Constant“ Apeiron,
Vol. 17, No. 2, April 2010 http://redshift.vif.com
Pfeufer,
J., (2001), On the Hypothesis of the Expansion of the
Earth,
in: Erzmetall 2001 Nr. 10
Rauner,
M., (2003), Das
Maß aller Massen. http://www.technik-channel.de/artikel/616496
Ruder,
H. et. al., (1990), Geodäsie
und Physik, in: Physikalische Blätter Nr 46, no. 2, S. 41 -
46
Sager,
G., (1976), Gedanken zur Expansion der Erde,
Beiträge zur
Meereskunde, Heft 37, Akademieverlag Berlin 1976
Schmutzer,
E., (2000), Approximate global treatment of the expansion
of
cosmic objects... in: Astr. Nachr. 321 (2000) 4
Stephani,
H.,
(1977),
Allgemeine Relativitätstheorie, Berlin: Dt. Verl.
d.
Wiss. 1977 S. 251
Zschau,
J., (1978),
Tidalfriction in the
solid Earth loading tides versus body tides, Aus: J.Südermann
/
P. Brosche (1978),
Tidalfriction and the Earth´s rotation Springer Verlag
Verwendete Sonderzeichen:
α
alpha
β
beta
γ
gamma
Δ
Delta
μ
my
π
Pi
Σ
Sigma
≈
ungefähr
≅
kongruent
→
gegen
± Plusminus-Zeichen
≤
kleiner gleich
≥
größer gleich
∞
unendlich